The following picture illustrates a not unusual situation of intersections, in which the various components are assumed to have various fundamental groups:

It helps here to have a theorem which immediately determines the fundamental groupoid of the union on these base points. Then one uses algebra and combinatorics to work out particular fundamental groups, if one wants them.
I came into groupoids by trying to find a new proof of the fundamental group of the circle. It turned out that one could do this using the fundamental groupoid on two base points. An analogous example, with a not so obvious universal cover, is the non Hausdorff space $X$ obtained from $[-1,1]\times \{-1,1\}$ by identifying all $(t, 1)$ with $(t, -1)$, except for $t=0$, as in the following picture:

Writing the 1968 edition of my book now called Topology and Groupoids (T&G) (available on amazon.com and e-version from my web site) convinced me that all of 1-dimensional homotopy theory was better expressed in terms of groupoids rather than groups, in that one obtained more powerful theorems with simpler proofs. Later results on the fundamental groupoid of orbit spaces (Chapter 11 of T&G) are more awkward to express in terms of groups; this elaborates on the point by Dustin Clausen. See further details below.
Henry Whitehead answered the question of "Why not restrict to CW-complexes with just one vertex?" by considering covering spaces. Philip Higgins gave a considerable generalisation of Grusko's theorem by considering covering morphisms of groupoids, see his 1971 book `Categories and groupoids' available as a TAC Reprint, 2005.
In 1966 I thought about prospective uses of groupoids in higher homotopy theory, and this led over many years to higher dimensional Seifert-van Kampen Theorems, with a range of new nonabelian calculations of second relative homotopy groups and triad homotopy groups (for the latter, see the "nonabelian tensor product of groups"). That sounds relevant to geometric topology!
So one answer to the original question is that the use of groupoids opens new worlds of possibilities.
Actually the idea of `change of base point for the fundamental group' is a bit bizarre: one does not describe a railway timetable in terms of return journeys and change of starting point for these! Why is this still taught to students?
In the end, an aesthetic viewpoint implies more power!
Thanks to those above who give me additional examples.
More information on my page From groups to groupoids.
September 2012: I forgot to add to this answer more information on orbit spaces, with particular reference to "two base points".
Ross Geoghegan in his 1986 review (MR0760769) of two papers by M.A. Armstrong on the fundamental groups of orbit spaces wrote: "These two papers show which parts of elementary covering space theory carry over from the free to the nonfree case. This is the kind of basic material that ought to have been in standard textbooks on fundamental groups for the last fifty years." At present, to my knowledge, "Topology and Groupoids" is the only topology text to cover such results.
Consider the action of the cyclic group of order 2, $Z_2$ on the unit circle $S$ by complex conjugation. Take $1$ as base point. The induced action of $Z_2$ on the fundamental group $\pi_1(S,1)$ is $n\mapsto -n$, and the quotient by this action is $Z_2$. But the quotient of $S$ by the action is a semicircle, which is contractible. What has gone wrong?
The problem is there are two fixed points of the action. The quotient of the action of $Z_2$ on the groupoid $\pi_1(S, A)$, where $A$ consists of the points $\pm 1$, is indeed correct.
The point is that a group acting on a space $X$ acts also on the fundamental groupoid $\pi_1 X$. If $X$ is Hausdorff, the action is properly discontinuous, and $X$ has a universal cover, then the fundamental groupoiud of the orbit space $X/G$ is the orbit groupoid of $\pi_1 X$. This is the groupoid expression of Armstrong's results. See Chapter 11 of Topology and Groupoids.
April 21,2013: The book Nonabelian algebraic topology: filtered spaces, crossed complexes, cubical homotopy groupoids gives an account of this new approach to basic algebraic topology at the border between homology and homotopy, without using singular homology theory, or simplicial approximation, but relying on the idea of multiple compositions of cubes. This also allows for results on second relative homotopy groups, results which, being essentially nonabelian, are not obtainable by traditional algebraic topology. It also avoids the "trick" of taking the free abelian group on ordered or oriented simplices in order to define chain groups, and the boundary map.
Note that that whereas group objects internal to groups are abelian groups, group objects internal to groupoids are in some sense "more nonabelian" than groups, as are groupoid objects internal to groupoids. So one looks to such objects to model higher homotopy properties: and this has been achieved.
October 2, 2014: I gave a talk on the "Intuitions for cubical methods in nonabelian algebraic topology" at the IHP, Paris, in June, 2014 to a workshop on "Constructive mathematics and models of type theory", and the handout version of the slides is available here. For me a main advantage of the excursion to groupoids is that it led me into thinking about higher versions, and how to express some key intuitions. The general question was:
"If groupoids are very useful in $1$-dimensional homotopy, can they be useful, or not, in higher homotopy?"
March 11, 2015
I hope the remarks of Grothendieck linked here as basepoints are found interesting.
Aug 4, 2015 A related discussion is at mathstackexchange.
September 15, 2015. have just found this paper:
arXiv:1508.03122 "Dynamics on Wild Character Varieties" Emmanuel Paul, Jean-Pierre Ramis Journal-ref: SIGMA 11 (2015), 068, 21 pages
It is relevant as it uses the fundamental groupoid on a set of base points in the context not of algebraic topology but of dynamical systems and differential equations.
September 19: Another point which comes out from the Paul-Ramis paper is the utility of preserving symmetry information. As another example. consider the following connected union of three spaces, with a set $S$ of chosen base points:

A description of $\pi_1(X,S)$ will preserve the symmetries of the situation, and this description may be needed for further investigations.
July 12. 2017 With regard to Daniel's point about knots, the following picture
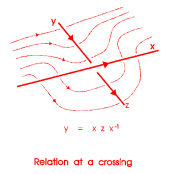
gives an intuition of the relation $y=xzx^{-1}$ at a crossing of a knot diagram. It is really a groupoid picture, and would seem to me to be more obscure if one tried to make it a picture about loops. To keep it, you could use two base points per crossing, one for "in" at top left and one for "out" at top right. I leave others to see if this is a helpful idea!
Philip Higgins told me of a dictum of his supervisor Philip Hall: "You should try to find an algebra which models the geometry, and not force the geometry into a particular algebraic mode simply because that mode is more familiar."
More background is in my 2018 Indagationes paper Modelling and Computing Homotopy Types: I.
October, 2019
The ideas of many base points to define fundamental groupoids is also relevant to the history of homotopy theory, which you can confirm from books on the history of topology (Dieudonn'e, James). In 1932 E. Cech gave a seminar to the ICM at Zurich on "Higher homotopy groups". He defined them and also proved they were abelian for $n \geqslant 2$. At that time a general interest among topologists was finding a higher dimensional version of the fundamental group, which of course was in general nonabelian. So the kings of topology of the time, Aleksandrov and Hopf, argued that Cech's definition could not be the "right" one; only a small paragraph appeared in the Proceedings, and Cech did no further work on the topic.
Later, interest came with publication in 1935 of papers by Hurewicz, and the study of homotopy groups became a central part of algebraic topology. We know the abelian nature of these groups as a result of "group objects in groups are abelian
groups". The idea of higher dimensional versions of the fundamental group was kind of discarded, though Henry Whitehead did mention in my hearing in 1957 that the early homotopy theorists were fascinated by the action of the fundamental group.
However Aleksandrov and Hopf were surely right! Now we know that "groupoids in the category of groupoids" can be more complicated than groupoids, and so on in higher dimensions. The fascination with the study of homotopy groups, which are defined only for spaces with base point, seems to have been a factor in ignoring the idea of a set of base points. The possible definition of strict higher homotopy groupoids seems to need more structure on a space, and so much work has taken place on the study of non strict higher homotopy groupoids. For a part of the story of the strict case, see my 2018 Indagationes paper referred to above.
Oct 1, 2020
I hope the following file Grothendieck of a Beamer presentation of a talk for a zoom conference on Grothendieck organised by John Alexander Cruz Morales and Colin McLarty for Aug 27-28 2020 will be helpful: it contains an extensive quote of Grothendieck's comments from my From groups to groupoids survey article and also suggestions of relations with Conway groupoids, and of uses of say thousands of base points.




