Let $P_1(n) := 1$ if $n=1$ and $\max_{q|n, \text{ }q\text{ prime}} q$ otherwise, denote the largest prime divisor of $n$.
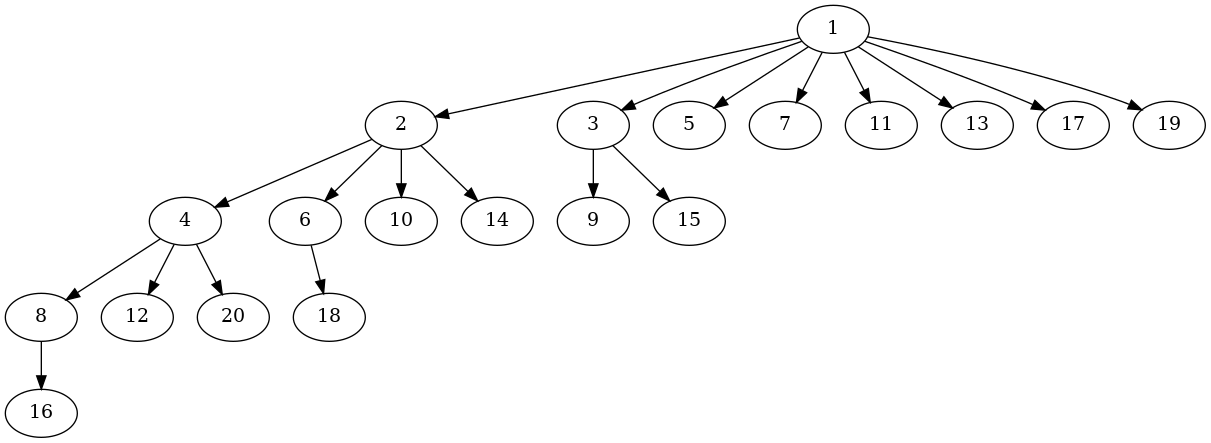
Let us define some rooted trees $T_{n,m}$ for $1 \le m \le n$ by:
- $T_{n,m}$ has as root the number $m$.
- If there are primes $p$ such that $P_1(m) \le p \le \frac{n}{m}$, then the children of $m$ are $T_{n,mp}$, otherwise $m$ is a leaf.
We set $T_n := T_{n,1}$. Here is an image of $T_{20}$:
We can encode these trees as parentheses $()$ or binary words $w_n$ $10$ where $(=1$ and $)=0$. Here are some words $n$ and $w_n$:
1
10
2
1100
3
110100
4
11100100
5
1110010100
From these words only it is possiblypossible to reconsctructreconstruct all prime factorizations of all numbers $1 \le m \le n$, without to have to factor any number $m$, only a check is needed if a number is prime or not.
Observing those words we see that they seem to be kind of random. To make this more precise, I suggest separating the $1$s and $0$s from each other by permutations $\sigma$ from $S_{2n}$, where $|w_n| = 2n$. This gives us a measure of its randomness, where we define the string for example:
$$0000000000111111$$
as being separated (the zeros than the ones), whereas the string:
$$010101010101010101$$
is not separated. In Diaconis & Graham & Knuth the following distance measure for permutations is suggested:
$$T(\pi,\sigma) = n - C(\pi^{-1} \sigma), \pi,\sigma \in S_n$$
where $C$ counts the number of distinct cyclces of the permutation. Using this, one can define the separation measure as for a arbitrary binary word $w$ as:
$$Z(w) = \max_{ \sigma \in S_{|w|}, \sigma \text{ separates } w} T(1,\sigma)$$
The standardized version $z(w_n):=z_n$ in the tree case, is given by Diaconis and Graham as :
$$z_n := \frac{Z(w_n)-\mu_n}{\sqrt{\operatorname{Var(n)}}} = \frac{|w|-C^*(w)-|w|+\log(|w |)}{\sqrt{\log(|w|)}}$$ which is equal to:
$$z_n=\sqrt{\log(2n)}-\frac{C^*(w_n)}{\sqrt{\log(2n)}}$$
where we have set: $C^*(w_n) := \max_{ \sigma \in S_{|w|}, \sigma \text{ separates } w}C(\sigma)$
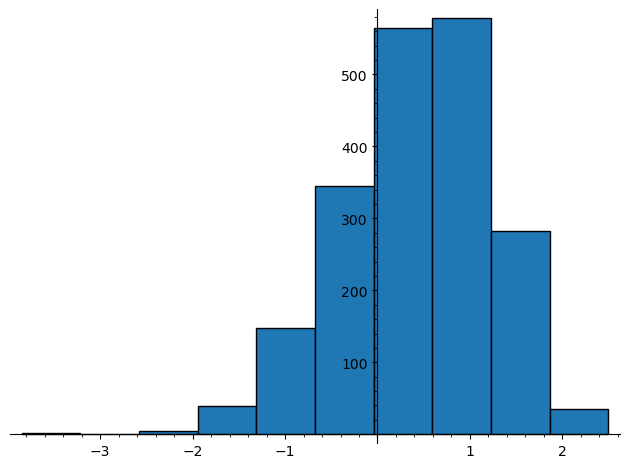
Question: Is it true that for $n \rightarrow \infty$ we have $z_n \approx N(0,1)$ is distributed as the standard normal variable?
Here is an image of the histogram for $1 \le n \le 2000$:
(Notice that in the image above I have not really computed $\max$ over all separating permutations but just taken one permutation given by the sorting algorithm.)