I guess a discrete-mathematics-related question is still welcome in MO since I was new to the community and learned from this amazing past post. The following claim is a simplified and abstract form of the network problem I am working on in distributed computing.
N.B.: all the graphs mentioned below are simple and undirected.
TL;DR
Does an $(x, bx)$-biregular graph always contain a $x$-regular bipartite subgraph?
Notation and Claim
A biregular or semiregular bipartite graph is a bipartite graph $G = (U, V, E)$ where the vertices in each bipartition $U$ or $V$ have the same degree. An $(x, y)$-biregular graph is a biregular graph $G = (U, V, E)$ where all vertices in $U$ have degree $x$ and the ones in $V$ have degree $y$ (from Wikipedia). We have $x|U| = y|V|$ immediately.
Let $|U| = ab$ and $|V| = a$. Then $bx = y$ and $1 \leq x \leq a$.
Claim. An $(x, bx)$-biregular graph $G = (U, V, E)$ always contains at least one $x$-regular bipartite subgraphs.
And the beauty of the claim is that if it holds, we are guaranteed to keep removing such a subgraph from $G$ by recursively applying the claim — an $(x, bx)$-biregular graph $G = (U, V, E)$ is now decomposed into $b$ edge-disjoint $x$-regular bipartite subgraphs.
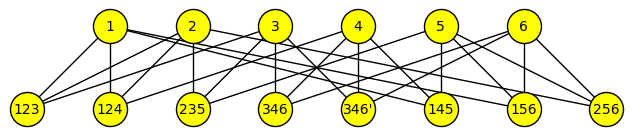
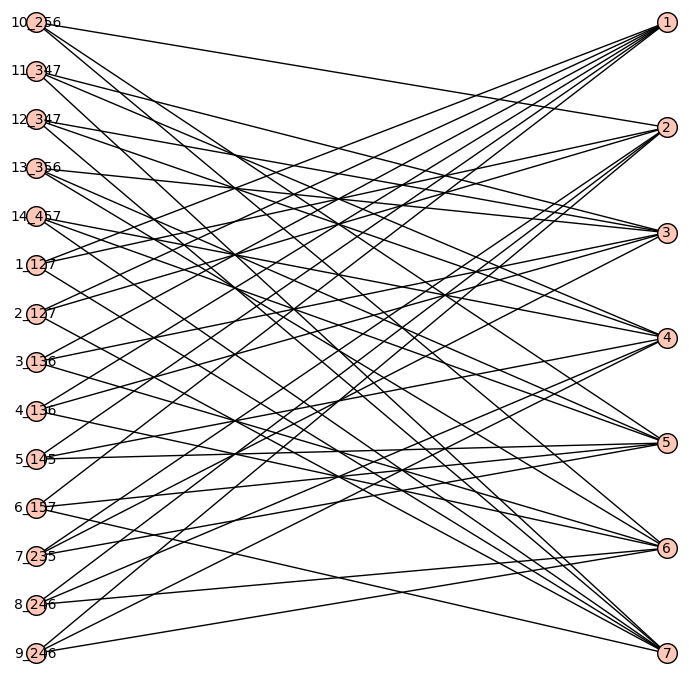
Here is a visual example with $a = 4$, $b = 3$ and $x = 2$ (hence $|U| = 12$ and $|V| = 4$). The edges with the same colour consist of a subgraph.
Some trivial cases:
- When $x = a$, meaning $G$ is complete and biregular, the claim holds.
- When $x = 1$, $G$ is disconnected but it is still the case.
- When $b = 1$, $G$ is a $x$-regular bipartite graph itself.
Possible Areas
After a long time online searching, I found three areas may be related to the claim potentially:
- Hypergraphs or family of sets: in such context, it can be paraphrased into that a multiple $x$-uniform $bx$-regular hypergraph with $abx$ hyperedges includes an $x$-uniform $x$-regular partial subhypergraph with $a$ hyperedges.
- Block design or more generally, combinatorial design: the claim now becomes that a 1-$(a, x, bx)$ design comprises a 1-$(a, x, x)$ sub-design; the sub-design is symmetric (the number of points equals the number of blocks) and not necessarily simple (no repeated blocks allowed).
- Algebraic graph theory: the adjacency matrix of a bipartite graph is quite unique, let alone that of a biregular one; with linear-algebraic or group-theoretic techniques, we may have a solution.
The Question
It is threefold:
- Do there exist some pre-existed results leading to the claim?
- Is there a better way to efficiently come up with a possible counter-example? I just wrote a Python script to randomly generate such a biregular graph and output a list of all its regular bipartite subgraphs by the brute-force search (to avoid any bias caused by heuristic algorithms). If someone is interested, I can link the script here.
- In order to prove/disprove the claim, which other mathematical fields are the most likely to be helpful here?
Thanks in advance from a computer scientist!