Eigenvalue estimates for operator perturbations

Question

I edited the question to a general mathematical question, since I found the answer in Carlo Beenakker's reference and think that my initial question was mathematically misleading.

What was behind all this was: If we take $W_N$ being trace free skew-symmetric matrices of rank $N$ on an $N$-dimensional space. And we perturb each of them with a positive operator $A_N$ such that all of the $A_N$ have the same trace. Is it true that as $N \rightarrow \infty$ the real part of some eigenvalue will tend to zero (resp. be zero)?

Answer:

The answer is yes by the following identity $$\operatorname{tr}(A_N)=\operatorname{Re}\operatorname{tr}(W_N+A_N) = \sum_{\lambda \in \sigma(W_N+A_N)} \operatorname{Re}(\lambda).$$

Since the left-hand side is finite, the right-hand side has to converge.

Answer 1

This problem of "non-Hermitian" quantum mechanics has been studied in the context of random-matrix theory (RMT), see for example the review Random matrix approaches to open quantum systems. The particular case pointed to in the OP is when the Hermitian matrix ${\cal H}=iW_{H}$ of high rank $N$ is perturbed by a positive-definite matrix $-i\pi WW^{t}$ of low rank $\delta N\ll N$. The eigenvalues $E_n-i\Gamma_n$ of the effective Hamiltonian ${\cal H}_{\text{eff}}={\cal H}-i\pi WW^t$ describe resonant scattering from a heavy atom or quantum dot (with $E_n$ the center of the resonance and $\Gamma_n$ its width). The special case in the OP where ${\cal H}$ is block-off-diagonal is referred to as the case of "chiral symmetry" in the context of random-matrix theory. (The appropriate ensemble for real ${\cal H}$ is the socalled "chiral orthogonal ensemble".)

Now the question in the OP is the distribution of the $\Gamma_n$'s in the limit $N\rightarrow\infty$ at fixed $\delta N$. The "universal" result of random-matrix theory (see section IV.A in the cited review) is that for $\delta N\ll N$ all $\Gamma_n$'s are greater than a minimal value $\Gamma_{\text{min}}\simeq\delta N/N$ and they accumulate near that value.
_{Note that the OP refers to $i$ times the eigenvalues of ${\cal H}$, so this approach to the real axis corresponds to an approach to the imaginary axis in the OP.}

Hence my answer to the final question of the OP, "does the spectrum approach the imaginary axis in the large-$N$ limit" is yes, it does, if the non-Hermitian perturbation has a rank $\delta N$ that remains small compared to the rank of the Hermitian part. There remains, however, for any finite $N$ a gap of order $\delta N/N$ that separates the "dissipative dynamics" from the unitary quantum mechanical evolution.

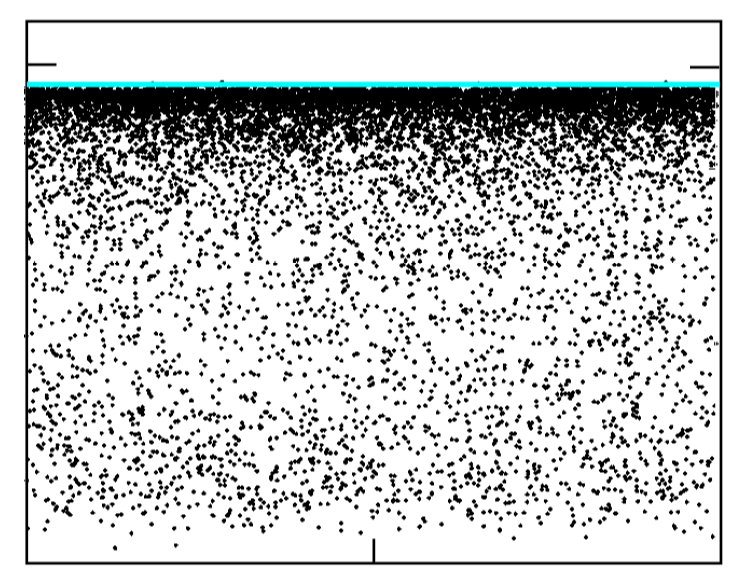
I show a plot that illustrates the clustering of the eigenvalues $E_n-i\Gamma_n$ of ${\cal H}_{\text{eff}}$ near the $\Gamma=0$ axis, with a sharp threshold (blue horizontal line) and a gap.
_{In the plot $N=500$ and $\delta N=50$. There is no chiral symmetry, but that would only introduce a $\pm E_n$ symmetry, it would not affect the gap in the $\Gamma$'s.}

source: arXiv:1405.6896