in this paper we have :
" On the Teichmüller tower of mapping class groups By Allen Hatcher at Ithaca, Pierre Lochak at Paris and Leila Schneps."
Definition. The maximal multicurve complex $H(\Sigma)$ is the two-dimensional cell complex having vertices the isotopy classes of maximal multicurves in $\Sigma$, with an edge joining two vertices whenever the corresponding maximal multicurves differ by a single S-move or A-move, and with faces added to fill in all cycles of the following five forms:...
exampl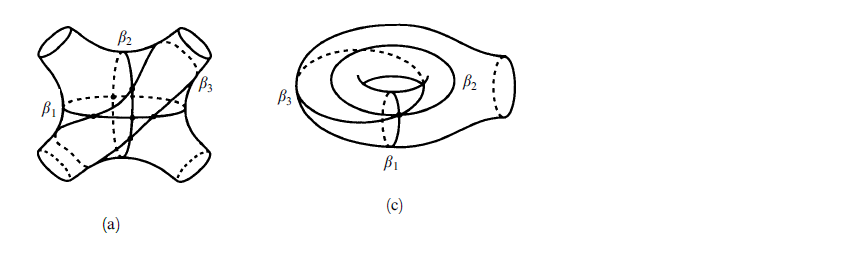e :
if $\Sigma$ has type $(0,4)$ or $(1,1)$, the two cases when a maximum multicurve contains just one circle, then $H(\Sigma)$ is the two-dimensional complex shown in figure 6 , consisting entirely of triangles since only the relations (3A) or (3S) are possible in these two cases. The vertices of $H(\Sigma)$ are labelled by slopes, which classify the nontrivial isotopy classes of circles on $\Sigma$. This is a familiar fact for the torus, where slopes are defined via homology. For the $(0,4)$ surface, slopes are defined by lifting curves to the torus via the standard two-sheeted branched covering of the sphere by
the torus, branched over four points which become the four boundary circles of the $(0,4)$
surface.
i can't understand this example . why maximal multicurve complex $H(\Sigma)$ for type $(0,4)$ or $(1,1)$ is figure $6$ ? why vertices of $H(\Sigma)$ are labelled by slopes ? why we draw hyperbolic triangle in Poincaré disk ?
I think this is help for me.also I think this is related to page 98 "farey complex "in A Primer on Mapping Class Groups Book by Benson Farb and Dan Margalit
