Folner sets and balls

Question

Several related questions were asked before on MO, but it is not clear to me if the following was settled.

Given a finitely generated amenable group, is it always possible to find some finite generating set such that some sequence of balls (w.r.t. the chosen set) is a Folner sequence?

Answer 1

This is not exactly an answer to the question, but is instead essentially a comment that was way too long for the comment space.

The OP mentioned that he doesn't have a good sense for the shapes of Følner sets in amenable groups of exponential growth. It seems that it might be helpful to give an example.

The simplest amenable group with exponential growth that I am aware of is the Baumslag-Solitar group $$ BS(1,2) \;=\; \langle a,b \mid bab^{-1} = a^2\rangle $$ The Cayley graph of this group is made of "sheets" of the following form: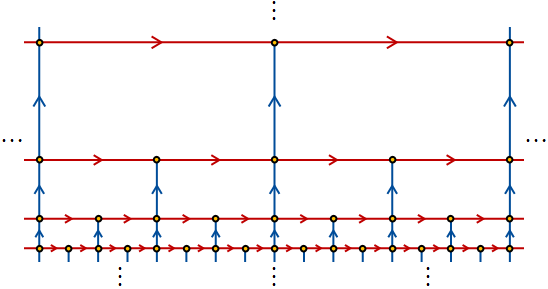

Here red edges correspond to the generator $a$, and blue edges correspond to the generator $b$. These fit together into a binary tree of (slightly offset) sheets:

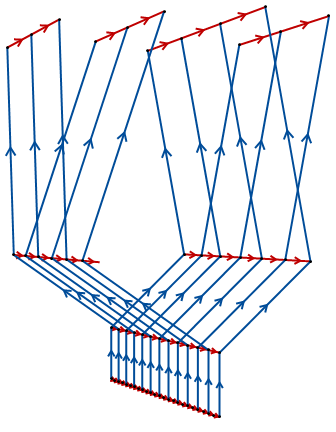
Note that each sheet is the 1-skeleton of a regular tiling of the hyperbolic plane. (This is the "sixth model" described Cannon, Floyd, Kenyon, and Parry in this paper). It follows that $BS(1,2)$ has exponential growth.

By the way, if you look at the whole Cayley graph from the "front", all of the sheets overlap, but no two vertices lie in the same position on the hyperbolic plane. What this means is that the elements of $BS(1,2)$ are in one-to-one correspondence with all the points $(x,y)$ in the hyperbolic plane for which $x$ is a dyadic fraction and $y$ is a power of $2$. Horizontal edges go from $(x,y)$ to $(x+y,y)$, and vertical edges go from $(x,y)$ to $(x,2y)$.

Now, even though $BS(1,2)$ has exponential growth, it turns out to be a solvable group. To see this, note first that $a$ has a sequence of roots $$ a^{1/2} \;=\; b^{-1}ab,\qquad a^{1/4} \;=\; b^{-2}ab^2,\qquad \ldots $$ The subgroup of $BS(1,2)$ generated by these roots is normal and is isomorphic to $\mathbb{Z}\bigl[\tfrac{1}{2}\bigr]$, the additive group of the dyadic fractions. Therefore $$ BS(1,2) \;\cong\; \mathbb{Z}\bigl[\tfrac{1}{2}\bigr] \rtimes \mathbb{Z} $$ where the $\mathbb{Z}$ is the cyclic subgroup generated by $b$. (This description is of course highly related to the "all in one plane" description of the Cayley graph given above.) This proves that $BS(1,2)$ is solvable, and hence amenable.

Now, the shapes of the balls in $BS(1,2)$ are roughly hyperbolic circles. (More precisely, the intersection of a ball with each sheet is roughly a hyperbolic circle). For example, the following picture shows the intersection of a ball of radius 9 with one sheet of the Cayley graph:

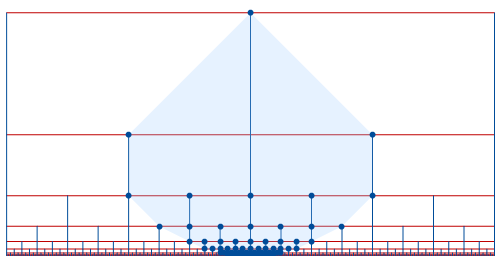
However, the Følner sets in $BS(1,2)$ look nothing like hyperbolic circles. The way to get a Følner set in $BS(1,2)$ is to choose a large "rectangle" in the Cayley graph: 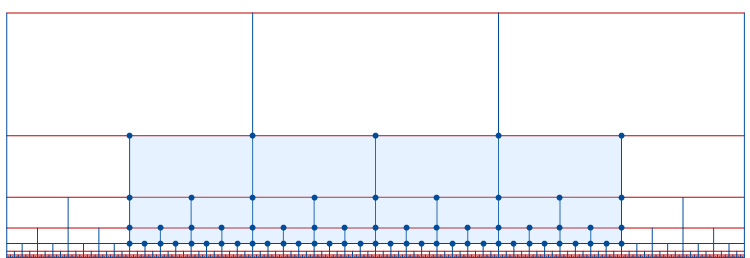This rectangle must also include the same region in all other "layers" of the Cayley graph that include the bottom edge. More precisely, let $$ R_{m,n} \;=\; \{(j/2^n,2^k) \mid -m\leq j/2^n \leq m\text{ and }-n\leq k\leq n\} $$ where we are referring to points in $BS(1,2)$ by their position in the hyperbolic plane. (So $R_{m,n}$ represents a rectangle of "width" $2m$ and "height" $2n$.) Then a sequence of such rectangles will be a Følner sequence as long as the width grows quickly relative to the height. In particular, it is easy to show that $$ |R_{m,n}| \;=\; (2^{n+1}m+1)(2n+1) $$ and $$ |\partial R_{m,n}| \;=\; 2(2^{n+1}m+1)+2(2^{2n+1}-1) $$ (where $\partial R_{m,n}$ denotes the set of boundary edges), so $$ \frac{|\partial R_{m,n}|}{|R_{m,n}|} \;=\; \frac{2}{2n+1} + \frac{2(2^{2n+1}-1)}{(2^{n+1}m+1)(2n+1)} \;\sim\; \frac{2}{2n+1} + \frac{2^{n+1}}{m(2n+1)} $$ where the first term comes from the vertical edges and the second comes from the horizontal edges. As you can see, this will be a Følner sequence as long as $m$ grows at least as quickly as $2^n$.

So the conclusion is that Følner sets in this Cayley graph are very wide rectangles, while the balls are roughly circle-shaped. I am skeptical that there would be any generating set for $BS(1,2)$ that has a subsequence of balls as a Følner sequence. Indeed, no matter what generating set you choose, large enough balls should still be roughly circle-shaped, which means they won't be "wide" enough to be Følner sets.

Answer 2

The question is still open (see below).

Partial answer 1: Here is a funny positive answer for "groups of pinched exponential growth". Let $B(n)$ be the ball of radius $n$ and $b_n = |B(n)|$. Let $S(n) = B(n) \setminus B(n-1)$ (with $S(0) = \lbrace e_G \rbrace$) be the spheres and $s_n = |S(n)|$.

Say a group has pinched exponential growth if there [is a generating set and there] are constants $K<L \in\mathbb{R}$ and $M \in \mathbb{R}$ so that $K \mathrm{exp}(Mn) \leq b_n \leq L \mathrm{exp}(Mn)$.

Let $g = \lim_n b_n^{1/n} = \inf_n b_n^{1/n}$. Now, note there are infinitely many $n_i$ so that, for $n \leq n_i$, $s_{n_i} \geq s_n$ (otherwise $s_n$ is bounded and $b_n$ grows at most linearly). Clearly, $s_{n_i} \leq b_{n_i} \leq (n_i+1) s_{n_i}$, so $$ g = \liminf b_{n_i}^{1/n_i} \geq \liminf_i s_{n_i}^{1/n_i}. $$ But $b_n \leq \sum_{j=0}^n s_j$ so $$g = \liminf_i b_{n_i}^{1/n_i} \leq \liminf (n_i+1)^{1/n_i} s_{n_i}^{1/n_i} = \liminf |S(n_i)|^{1/n_i}. $$ Thus far we have $$g = \liminf |S(n_i)|^{1/n_i}.$$ However, $n \mapsto s_n$ is also sub-multiplicative, i.e. $s_{n+m} \leq s_n s_m$. Hence $$g = \lim_n s_n^{1/n} = \inf_n s_n^{1/n}.$$ The equality with the $\inf$ implies $s_n/g^n \geq 1$.

Next note that pinched exponential growth is equivalent to $\limsup b_n/g^n = L < \infty$ (for some $L$). Putting this together $$ \begin{array}{rll} \displaystyle \liminf \frac{s_{n+1}}{b_n} & \displaystyle = g \liminf \frac{s_{n+1}}{g^{n+1}} \cdot \frac{g^n}{b_n} \\ & \displaystyle \geq g \liminf \frac{s_{n+1}}{g^{n+1}} \bigg( \limsup \frac{b_n}{g^n} \bigg)^{-1} & \displaystyle \geq g /L \end{array} $$ This implies that $$ \frac{ |B(n+1)|}{|B(n)|} \geq 1 + \frac{g}{L} $$ as desired.

2 remarks on pinched exponential growth:

1- the property depends on the generating set. If $(G,S)$ has pinched exponential growth. Then $G \times \mathbb{Z}$ with "summed" generating set $\lbrace (s,0) \mid s \in S \rbrace \cup \lbrace (e_G,\pm 1) \rbrace$ has also pincehd exponential growth. With the "product" generating set $\lbrace (s,\epsilon) \mid s \in S , \epsilon = \pm 1 \rbrace$ it does not have pinched growth. Also, $G \times G$ with the product generating set has pinched exponential growth, but with the summed generating set it does not.

2- with the usual generating sets, solvable BS and some lamplighters groups have pinched exponential growth (this can be seen on their growth series, see below).

The question is open, it seems however that the answer is widely believed to be "no". For example, this is claimed in [de la Harpe, Topics in geometric group theory] see section VII.C on page 205. The proof is not included in the book but a reference to a paper is given. However, this reference only shows that if there is a subsequence $\lbrace n_i \rbrace$ so that the $B_{n_i}$ is a Folner sequence, then the integers $\lbrace n_i \rbrace$ have density $0$.

[EDIT: the density of a subset $S$ of the positive integers is $\liminf |S_i|/i$ where $S_i = S \cap [1;i]$.]

After sending a few emails, it was confirmed that the question is still open.

It is also relatively easy to see that a group has subexponential growth if and only if there is a density 1 sequence $\lbrace n_i \rbrace$ so that the associated sequence of balls is Folner.

Partial answer 2: here is another answer under a very strong assumption. If the group has a rational growth series (which is the case for $BS(1,n)$ and many lamplighter groups over $\mathbb{Z}$), then [$b_{n+1}/b_n$ need not converge but] one can check that $\liminf \frac{b_{n+1} - b_n}{b_n} > 0$.

For the growth series of $BS(1,n)$ see Collins, Edjvet and Gill, Growth series of the group $\langle x,y \mid x^{-1}y x=y^\ell \rangle$, Arch. Math. 62:1-11, 1994. For the growth series of lamplighters of the form $(\oplus_{i \in \mathbb{Z}} H) \rtimes \mathbb{Z}$) where the growth series of $H$ is known (i.e. $H$ is finite, or Abelian, or $BS(1,n)$, or a lamplighter or ...) see Johnson, Rational growth of wreath products, in "Groups St Andrews 1989" volume 2 309--315

Answer 3

I don't believe that groups with exponential growth can have a Folner sequence of balls. Here's my reasoning.

Exponential growth implies that there is a constant $c$ such that $$ \left| \delta B_t \right| \geq c \left| B_t \right|.$$

Suppose that $G$ is a group of exponential growth with $m$ generators. Then, by the pigeonhole principle, there must be a generator $g$ so that $$\left| g(\delta B_t) \cap \delta B_{t+1} \right| \geq \frac{1}{m} \left|\delta B_{t+1} \right| \mbox{, i.o.}$$

Now, since $g(\delta B_t) \cap \delta B_{t+1} \subseteq gB_t \vartriangle B_t$, we have $$ \frac{ |gB_t \vartriangle B_t|}{|B_t|} \geq \frac{\left| g(\delta B_t) \cap \delta B_{t+1} \right|}{|B_t|} \geq \frac{c}{m}, \mbox{ i.o.}$$

See also A. Nevo, "Pointwise ergodic theorems for actions of groups," Handbook of Dynamical Systems, 1B.