Let $G := \langle a, b, c \rangle < {\rm Sym}(\mathbb{Z}^2)$ be the group generated by the permutation $$ a: \ (m,n) \ \mapsto \ (m-n,m) $$ of order $6$ and the involutions $$ b: \ (m,n) \ \mapsto \ \begin{cases} (m,2n+1) & \text{if} \ n \equiv 0(\text{mod} \ 2), \\ (m,(n-1)/2) & \text{if} \ n \equiv 1(\text{mod} \ 4), \\ (m,n) & \text{if} \ n \equiv 3(\text{mod} \ 4) \\ \end{cases} $$ and $$ c: \ (m,n) \ \mapsto \ \begin{cases} (m,2n+3) & \text{if} \ n \equiv 0(\text{mod} \ 2), \\ (m,(n-3)/2) & \text{if} \ n \equiv 3(\text{mod} \ 4), \\ (m,n) & \text{if} \ n \equiv 1(\text{mod} \ 4). \\ \end{cases} $$ Drawing spheres of radius $r$ about $(0,0)$ for "large enough" $r$ reveals fractal-like structures.
Added on July 28, 2014: A video showing more pictures is now available on YouTube here. The video starts with a sequence showing entire spheres of small radii, i.e. from $r = 8$ to $r = 24$, and continues with pictures showing smaller parts of spheres of larger radii up to $r = 45$. Monochrome pictures show only one sphere, respectively, a part thereof; colored pictures show multiple spheres in different colors.
Added on March 16, 2014: Pictures of the spheres of radius $30$ and $36$ can be downloaded here:
Radius 30 (3487 x 3079 pixels, 111KB), Radius 36 (10375 x 9103 pixels, 693KB).
Sample snippets of the large -- about $200$ megapixels at $r = 38$ to about $3$ gigapixels at $r = 45$ -- pictures are (black pixel = belongs to sphere, white pixel = doesn't belong to sphere):
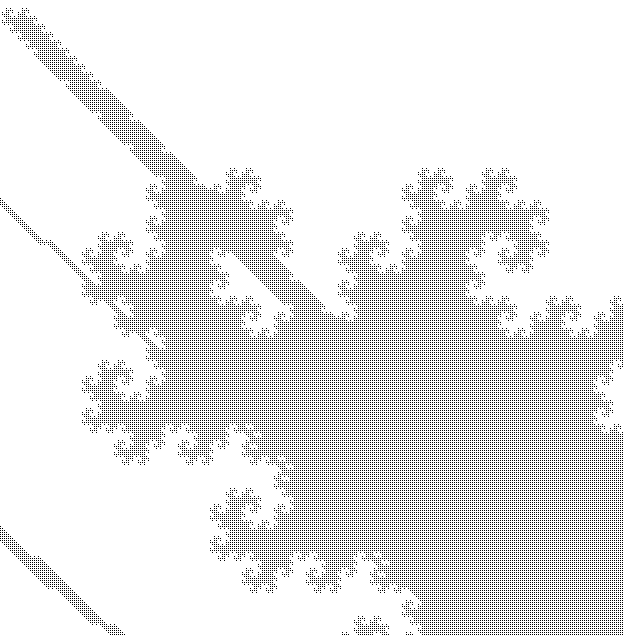
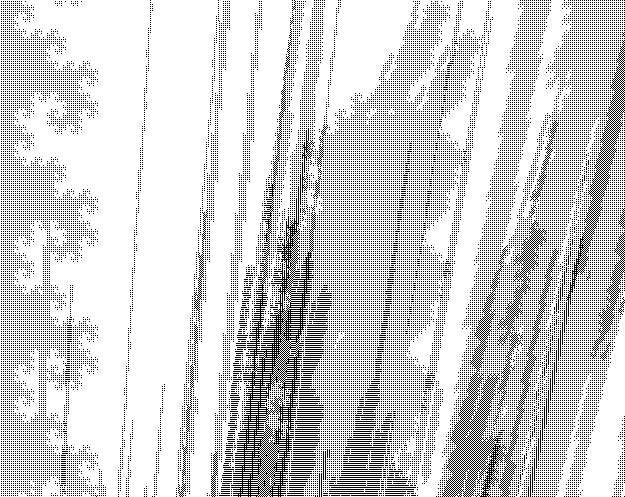
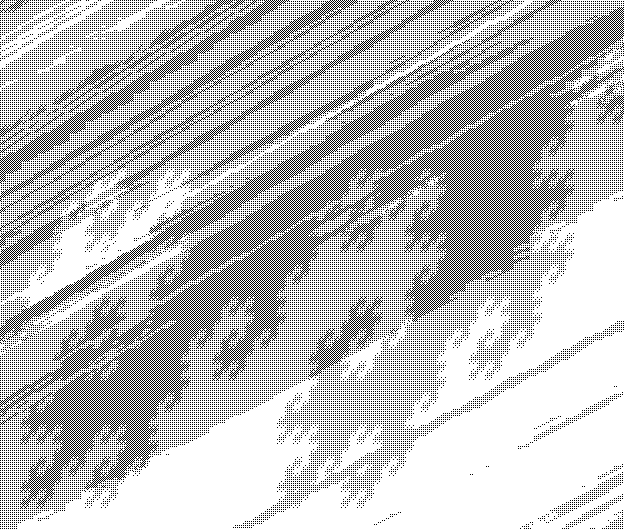
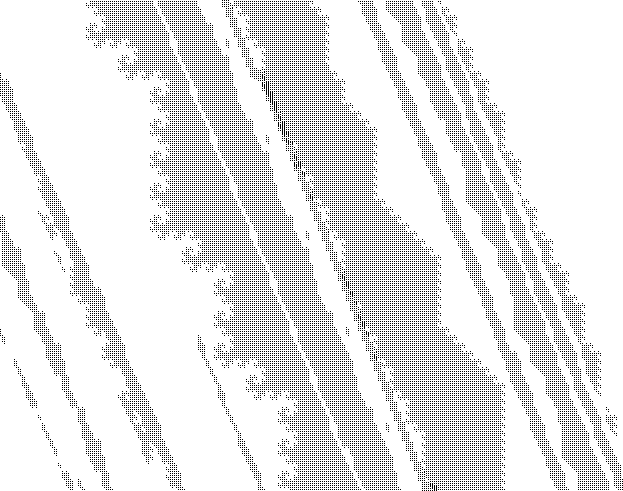
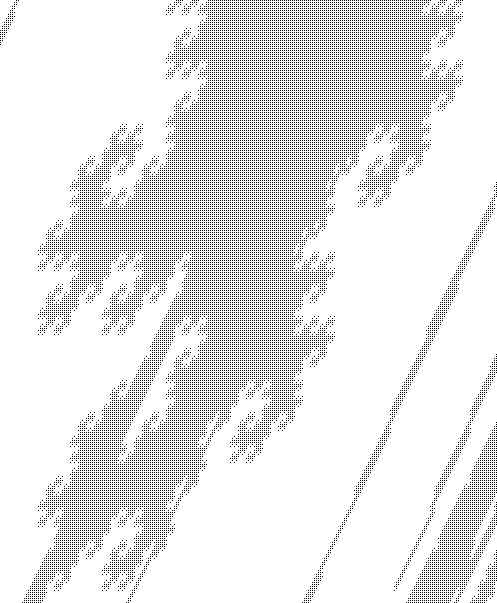
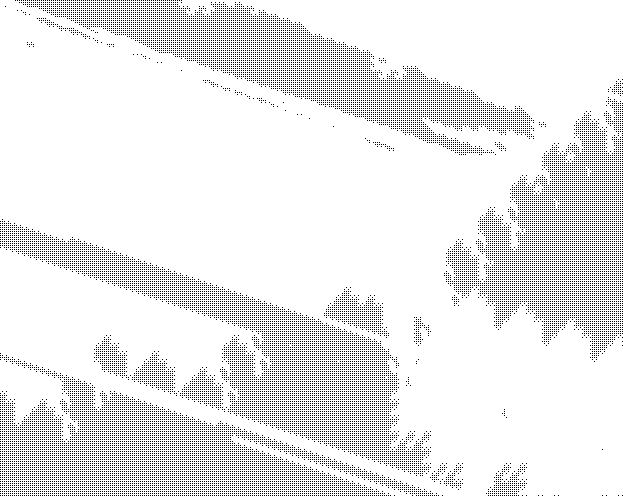
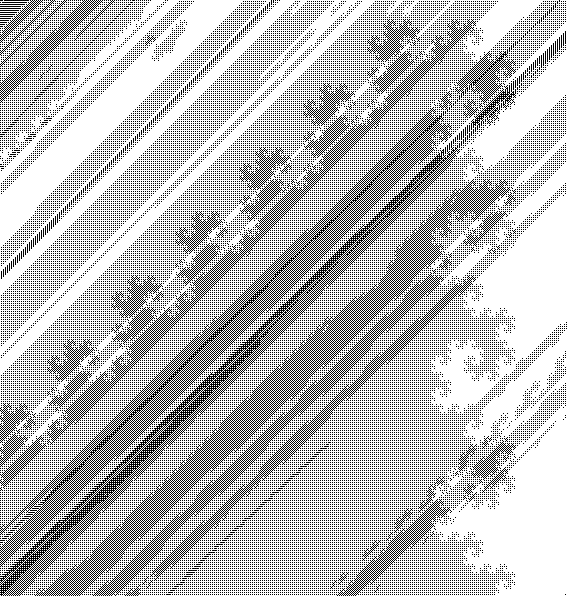

The images above show parts of the spheres of radius $38$, $40$ and $45$.
Question: How can the observed patterns be explained?
Remark 1: The cardinalities of the spheres of radii $r = 0, \dots, 45$ about $(0,0)$ are
1, 2, 4, 8, 14, 26, 39, 68, 114, 188, 289, 404, 560, 827, 1341, 2052, 3158, 4540,
6091, 8630, 12241, 17739, 27727, 41846, 61234, 86647, 117806, 163795, 233939, 340659,
523862, 768739, 1110855, 1569204, 2148377, 2994661, 4287462, 6195498, 9389566,
13568954, 19542862, 27619364, 38048372, 53304607, 76433012, 109839303.
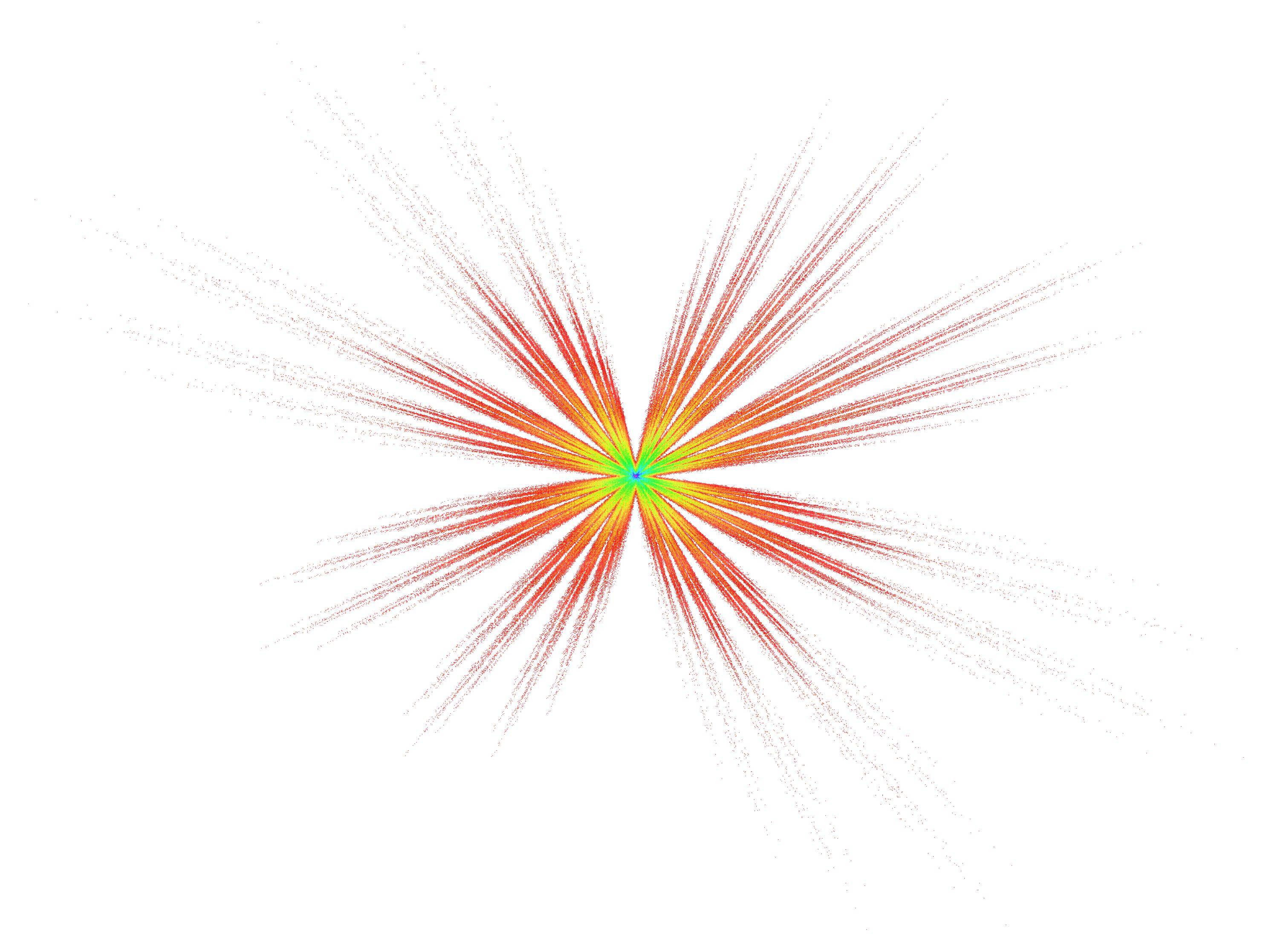
The entire sphere of radius $20$ looks as follows (the overall shape of the larger spheres is roughly similar):
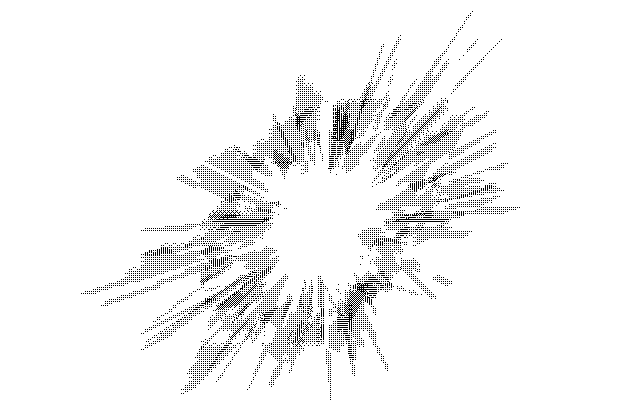
Added: At a scale of about $1:100$, the entire sphere of radius $45$ looks as follows:

Remark 2: In the notation of this and this question, $b$ and $c$ induce on the second coordinate the class transpositions $\tau_{0(2),1(4)}$ and $\tau_{0(2),3(4)}$, respectively. Further, in the notation of (1) and (2) we have $G < {\rm RCWA}(\mathbb{Z}^2)$.