Gluing faces of n-cube

Question

Assuming $C_n$ be the $n$-cube, the intersection of $C_n$ with a supporting hyperplane $H(P, v)$ is called a face or more precisely a $d$-face if the dimension is $d$.

Let $f_0$ and $f_1$ be faces with the same dimension $d$, we say $f_0$ and $f_1$ are gluing together is defined as follows:

1. when $f_0$ and $f_1$ are 0-faces, we say they are gluing together if we identify the vertices $f_0$ and $f_1$ to obtain a single vertice.
2. when $f_0$ and $f_1$ are d-faces, we say they are gluing together if they have the same $d-1$ faces and then we identify $f_0$ and $f_1$.

$f_0,\dotsc,f_s$ are gluing together if $f_0,\dotsc,f_{s-1}$ are gluing together to be $f_t$ and then we glue $f_t$ and $f_s$.

We say $A$ is $C_n$-glued if A is obtained by gluing faces in $C_n$ together.

For example, $C_2$ is a square and we may glue one fixed point and its antipode point together to obtain a $C_2$-glued $A_0$, we could also glue one fixed point and its antipode point together and then glue the adjacent edge together to obtain another $C_2$-glued $A_1$.

I want to know how to describe all $C_n$-glued objects for some $n$, a simpler question might be the number of $C_n$-glued up to symmetries for any $n$. The number of $C_1$-glued is 2 and the number of $C_2$-glued is 19 up to symmetries and we count the trivial one who does nothing.

EDIT: Too long to be a comment: I may show the 19 $C_2$-glued "objects".

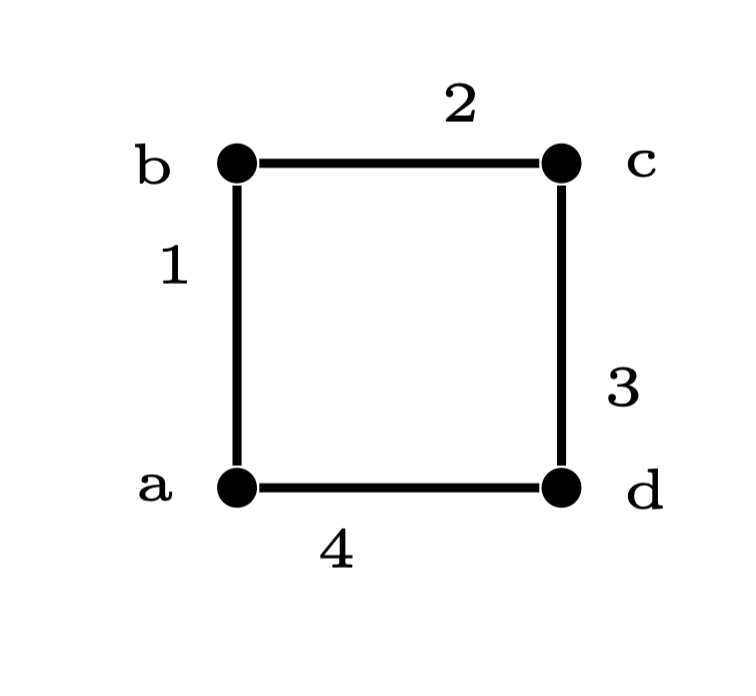
$C_2$ is a square, its vertices are a, b, c, and d and its edges are 1, 2, 3, and 4. We write $[xyz,uv]$ for the object obtained by gluing $x, y, z$ together and gluing $u, v$ together. The 19 $C_2$-glued "objects" are $C_2$ itself, $[ab]$, $[ac]$, $[ab, cd]$, $[ac, bd]$, $[abc]$, $[abcd]$, $[ac, 12]$, $[ac, 12, 34]$, $[ab, cd, 24]$, $[ac, bd, 24]$, $[ac, bd, 13, 24]=[ac, bd, 123]$, $[ac, bd, 1234]$, $[abc, 12]$, $[abc, 34]$, $[abc, 12, 34]$, $[abcd, 12]$, $[abcd, 12, 34]=[abcd, 123]$, $[abcd, 1234]$.