3
$\begingroup$

Looking on the growth function for Rubik's group and symmetric group, one sees rather different behaviour:

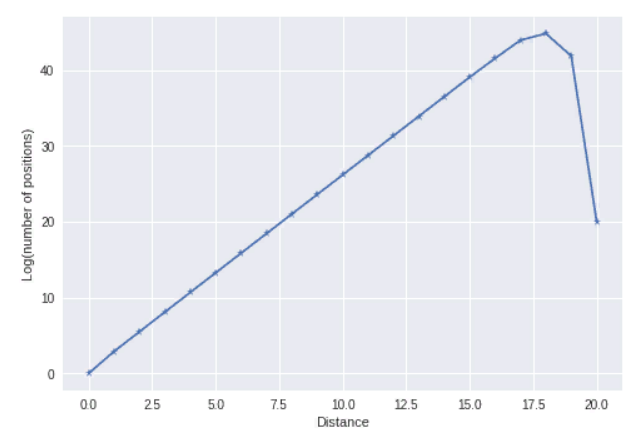
Rubik's growth in LOG scale (see MO322877): Rubik's growth in LOG scale

S_n n=9 growth and nice fit by normal distribution (NOT log scale): S_n n=9 growth and nice fit by normal distribution (NOT log scale)

As usually growth function of $n$ - is number of elements which can be represented by product of $n$ generators and cannot by less number. For symmetric group we take standard generators - adjacent permutations (and so code below uses the fact that length equals to inversion number), for Rubik's group also standard generators - see MO322877. The rough explanation behind such difference is that S_n and its generators is more like an abelian group, while generators of Rubiks group behave like a free group up to certain order and than cutted by relations of quite a long length. For abelian groups like $(Z/2Z)^n$ grows corresponds to normal distribution by the most classical central limit theorem (see bean machine video), normal distribution approximation often happens for various metrics on $S_n$ - see MO320497

Informal question what can a be a something like a typical growth for finite groups ? For example take "small group library of GAP" what is typical there ?

Question 2 Can computer algebra systems like GAP or MAGMA compute such a growth for finite groups and given set of generators ? At least for "small group library" ? What algorithms are used ?

I understand there is huge literature on Cayley graphs of groups e.g. Harald A. Helfgott,BAMS, 2015, Growth in groups: ideas and perspectives (see also MO102737), still I wonder:

Question 3 What are some other nice surveys which concentrates on finite groups Cayley graphs and growth functions ?

PS

Here is old discussion of similar spirit: What relationship, if any, is there between the diameter of the Cayley graph and the average distance between group elements? what is "typical" relation between diameter median - taking Rubik's cube and S_n as examples

PSPS

Here is Python3 code for $S_9$ growth calculation and normal fit. (One can use https://colab.research.google.com/ for free - you even do not need to install anything on your comp - use browser and code runs on google's servers: 

def inversion(permList): # http://code.activestate.com/recipes/579051-get-the-inversion-number-of-a-permutation/
    """
    Description - This function returns the number of inversions in a
                  permutation.
    Preconditions - The parameter permList is a list of unique positve numbers.

    Postconditions - The number of inversions in permList has been returned.

    Input - permList : list
    Output - numInversions : int
    """
    if len(permList)==1:
        return 0
    else:
        numInversion=len(permList)-permList.index(max(permList))-1
        permList.remove(max(permList))
        return numInversion+inversion(permList)

import matplotlib.pyplot as plt
import time 

import scipy
import scipy.stats
import numpy as np


# Get all permutations  # https://www.geeksforgeeks.org/permutation-and-combination-in-python/
# using library function 
from itertools import permutations # import lib
n = 9
lst = range(1,(n+1) ) # =  [1, 2, 3, 4, 5, 6, 7,..., n]
perm = permutations(lst) # all n! permutations are here

list_i = [] # Store all inversion numbers here 
v = np.zeros(int( n*(n+1)/2) )  # histogram for inversion numbers here
start_time = time.time()
for p in list(perm): # Loop over permutations
  inv_count = inversion(list(p))  
  v[inv_count] += 1 
  list_i.append(inv_count) # 

print('n=',n, time.time() - start_time  , 'seconds passed' )
print('Mean' , np.mean( list_i), 'Std ', np.std( list_i) )    

y = v / np.sum(v)  # normalize histogram
plt.plot(y,'*-',label = 'Length Distribution')

# Fit by normal part:
dist = getattr(scipy.stats, 'norm')
param = dist.fit(np.array(list_i) ) # https://glowingpython.blogspot.com/2012/07/distribution-fitting-with-scipy.html
x = np.linspace(0,int( n*(n+1)/2),int( n*(n+1)/2)+1)
# fitted distribution
pdf_fitted = scipy.stats.norm.pdf(x,loc=param[0],scale=param[1]) # https://glowingpython.blogspot.com/2012/07/distribution-fitting-with-scipy.html
plt.plot(x,pdf_fitted,'d-', label = 'Fit by normal')
plt.legend()
plt.title('S_n n= '+str(n) )
plt.show()
Improve this question
$\endgroup$
2
  • $\begingroup$ If you make experiments, you might try with $S_n$ with a random pair. Indeed, random pairs are generically generating, and the behavior for growth is known to be very different from "obvious" generating pairs such that the pair $\{(12),(123\dots n)\}$, notably they have a smaller diameter. (Still I don't know if for such a given group as $S_9$ the "generic" behavior is already preponderant.) $\endgroup$
    – YCor
    Feb 24, 2019 at 22:47
  • $\begingroup$ @YCor thank you ! So from your comment and reading JSE and Tao mathoverflow.net/a/61495/10446 it seems that randomly chosen elements should give something like an expander graph and that should be different from standard generators of S_n picture. It is interesting whether properties mentioned by JSE fullfils for Rubik's cube... $\endgroup$
    – Alexander Chervov
    Feb 27, 2019 at 18:11

0

Reset to default

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.