Definition 1. An affine plane is a pair $(X,\mathcal L)$ consisting of a set $X$ and a family $\mathcal L$ of subsets of $X$ called lines which satisfy the following axioms:
Any distinct points $x,y\in X$ are contained in a unique line $L\in\mathcal L$;
Any line $L\in \mathcal L$ contains at least three points;
$X\notin \mathcal L$;
For every line $L\in\mathcal L$ and point $x\in X\setminus L$ there exists a unique line $\Lambda\in\mathcal L$ such that $x\in \Lambda$ and $\Lambda\cap L=\emptyset$.
For two distinct points $x,y\in X$ of an affine space $(X,\mathcal L)$ by $\overline{xy}$ we denote the unique line containing the points $x,y$.
Two lines $A,B\in\mathcal L$ are called parallel (denoted by $A\parallel B$ ) if either $A=B$ or $A\cap B=\emptyset$.
An affine plane $(X,\mathcal L)$ is finite if the set $X$ is finite.
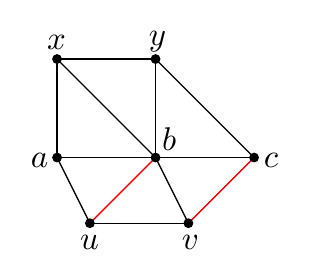
Definition 2. An affine plane $(X,\mathcal L)$ is defined to have the Doubling Property if for every distinct points $a,b\in X$ and points $c\in\overline{ab}$ and $u,v,x,y\in X\setminus\overline{ab}$, the parallelity relations $\overline{xy} \parallel \overline{ab} \parallel \overline{uv}$, $\overline{ax} \parallel \overline{by}$, $\overline{xb} \parallel \overline{yc}$, $\overline{au} \parallel \overline{bv}$, imply $\overline{ub} \parallel \overline{vc}$.
In affine planes with the Doubling Property we can duplicate the ``distances'' (in a suitable sense, of course).
Question. Is there a finite affine space without the Doubling Property?
It can be shown that the Doubling Property follows from the well-known
Little Desargues' Axiom: for every parallel lines $A,B,C$ and points $a,a'\in A\setminus(B\cup C)$, $b,b'\in B\setminus(A\cup C)$, $c,c'\in C\setminus(A\cup B)$, the parellelity relations $\overline{ab} \parallel \overline{a'b'}$ and $\overline{bc} \parallel \overline{b'c'}$ imply $\overline{ac} \parallel \overline{a'c'}$.
On the other hand, the Moulton plane does not have the Doubling Property. But the Moulton plane is infinite.