8
$\begingroup$

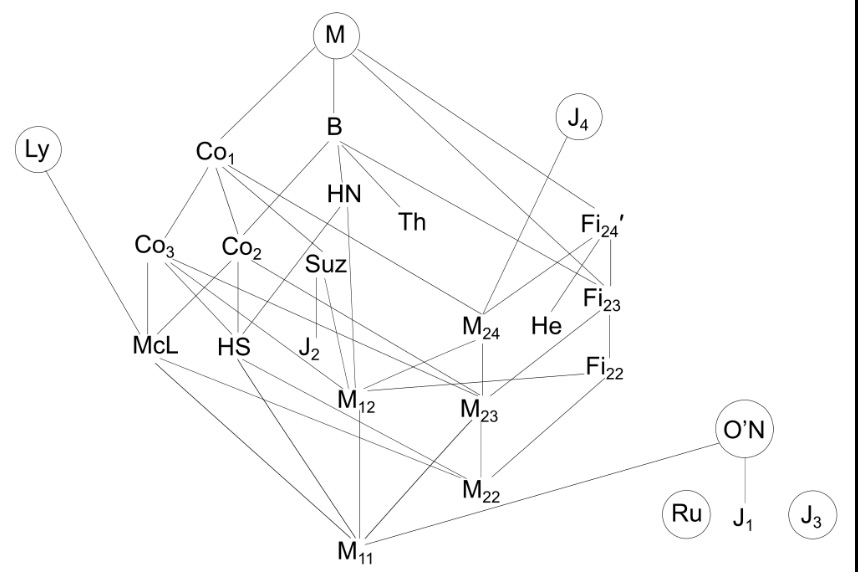
Edit: I was able to make a 3D diagram of the happy family if anyone is interested!

https://www.youtube.com/watch?v=_4IjnIcECoQ

I'm working on a twitter thread about the monster group, because I saw an interview with John Conway and he was very interested in the monster group.

Here is a link to the wikipedia article on the monster: https://en.wikipedia.org/wiki/Monster_group

I'm very interested in the diagram of the sporadic groups. (Also if anyone would like to provide some basic understanding of the sporadic groups that would be helpful.) I'm trying to make a 3D version of the diagram with wire...

When I look at the diagram sproadic groups diagram

I can understand that the sporadic groups that are maximal are the ones that are circled. And $M$ is the monster, with $B$ the baby monster. And it looks like $J_1$ is a subquotient of the maximal group $O'N$. I'm not very familiar with subquotients, so I am wondering if $J_1$ is a subquotient of $M$? That is, for my purposes, do I need to include $O'N$ and $J_1$ in the diagram of the monster?

Improve this question
$\endgroup$
17
  • 2
    $\begingroup$ Note for readers: the diagram (copied from the Wikipedia page) represents the "be isomorphic to a subquotient of" relation. More precisely I guess that there an edge between $A$ and $B$ with $A$ below $B$ if $A$ is isomorphic to a subquotient of $B$, and there's no other sporadic group "in between", but the caption is not more precise than "showing subquotient relationship". $\endgroup$
    – YCor
    Apr 18, 2020 at 9:07
  • 1
    $\begingroup$ Curious: "Code golf" on Monster group: codegolf.stackexchange.com/questions/203524/conways-monster $\endgroup$
    – Alexander Chervov
    Apr 18, 2020 at 9:09
  • 1
    $\begingroup$ By the way I guess that it might happen that there are other simple groups "in between". That is, a non-sporadic simple group involved in some larger sporadic group, and involving some smaller sporadic group. $\endgroup$
    – YCor
    Apr 18, 2020 at 9:10
  • 1
    $\begingroup$ @YCor I haven't checked thoroughly but I don't believe that there are any examples in the diagram where there are any other simple groups in between, but they are not all maximal subgroups, and some are genuinely quotients of subgroups. For example, it is the double cover $2.{\rm B}$ rather than ${\rm B}$ itself that is a subgroup of M, and the extension $2^{11}.{\rm M }_{24}$ is a maximal subgroup of ${\rm J}_4$. $\endgroup$
    – Derek Holt
    Apr 18, 2020 at 9:19
  • 2
    $\begingroup$ Nice sculpture!! It's cool to see such abstract theory represented physically... $\endgroup$
    – Nick Gill
    Apr 24, 2020 at 12:31

1 Answer 1

Reset to default
15
$\begingroup$

No $J_1$ is not involved in (i.e. is not a subquotient of) the Monster.

The six sporadic simple groups listed here as "Pariahs" are precisely those that are not involved in the Monster, namely $J_1$, O'N, $J_3$, Ru, $J_4$, Ly.

There is a lot of information about the Monster and its subgroups in Section 5.8 of Robert Wilson's book, "The Finite Simple Groups''.

Note that, apart from a few uncertainties about a few possible groups ${\rm PSL}_2(q)$ for some small values of $q$, the maximal subgroups of the Monster are now all known, so locating which other simple groups are involved in it is moderately straightforward, using the ATLAS of Finite Simple Groups or the weblink above.

In fact Robert Wilson proved in a 1986 paper "Is $J_1$ a subgroup of the Monster" in Bull. London Math. Soc. 18, 349-150 that $J_1$ is not a subgroup, which was much more difficult at the time, because much less was known about the maximal subgroups of the Monster.

Improve this answer
$\endgroup$
9
  • $\begingroup$ Thank you very much, this is very interesting and helpful! $\endgroup$
    – user141903
    Apr 18, 2020 at 14:59
  • 1
    $\begingroup$ If $A$ is a subquotient of $B$ then is $A$ necessarily a subgroup of $B$? If $A$ is a subgroup of $B$ then it seems it is automatically a subquotient of $B$. Is that true? $\endgroup$
    – user141903
    Apr 21, 2020 at 18:11
  • 2
    $\begingroup$ Yes if $A$ is a subgroup of $B$ then it is automatically a subquotient of $B$. But the converse is not true. For example (as I said in a previous comment), the Baby Monster ${\rm B}$ is a subquotient of ${\rm M}$, but it is not a subgroup. It is the double cover $2.{\rm B}$ that is a subgroup of ${\rm M}$. $\endgroup$
    – Derek Holt
    Apr 21, 2020 at 18:23
  • $\begingroup$ Great! Woah, I have no idea what the "double cover 2.B that is a subgroup of $M$" means, but that sounds so interesting. Also, have you ever seen a 3D model of the happy family diagram? I made one and it looks pretty neat! $\endgroup$
    – user141903
    Apr 21, 2020 at 18:57
  • 1
    $\begingroup$ @Erin it means that there is a 2-1 surjective group homomorphism $2.B \to B$ (using the notation used in the ATLAS), and an injective homomorphism $2.B \to M$. In particular, $2.B$ has $C_2$ as a central subgroup, hence isn't simple, but $B \simeq 2.B/C_2$ is simple. $\endgroup$
    – David Roberts ♦
    Apr 24, 2020 at 4:09

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.