9
$\begingroup$

$\DeclareMathOperator{\id}{\mathrm{id}}\DeclareMathOperator{\Hom}{\mathrm{Hom}}\DeclareMathOperator{\UnCoNat}{\mathrm{UnCoNat}}\DeclareMathOperator{\UnNat}{\mathrm{UnNat}}\DeclareMathOperator{\CoNat}{\mathrm{CoNat}}\DeclareMathOperator{\Nat}{\mathrm{Nat}}$The set of natural transformations between two functors $F,G\colon C\to D$ is computed by the formula $$\Nat(F,G)\cong\int_{A\in C}\Hom_D(F(A),G(A)).$$ I've been wondering recently about the dual of this notion, that of the set of "natural cotransformations" from $F$ to $G$, defined by $$\CoNat(F,G)\cong\int^{A\in C}\Hom_D(F(A),G(A)).$$ Explicitly, this is the quotient of the set $\coprod_{A\in C}\Hom_D(F(A),G(A))$ by the equivalence relation generated by the relation $\sim$ identifying two maps $\alpha_{A},\beta_A\colon F(A)\to G(A)$ whenever there exist

  • A morphism $f\colon A\to B$ of $C$;
  • A morphism $\phi\colon F(B)\to G(A)$ of $D$; making the diagrams

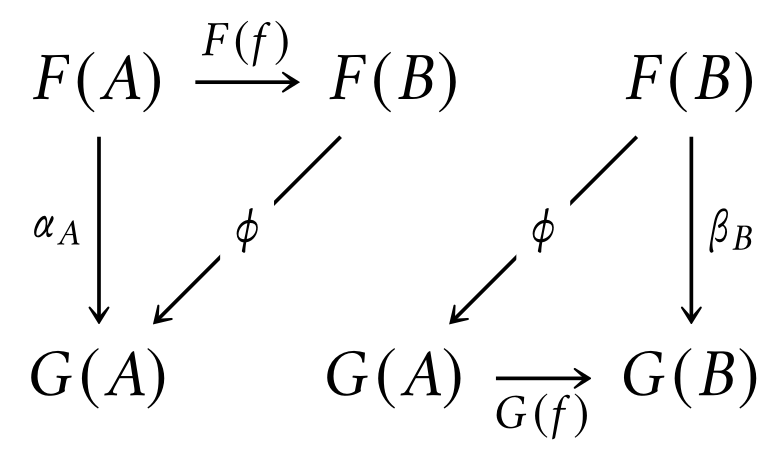
commute. For example, $\CoNat(\id_C,\id_C)$ recovers the trace of $C$.

Now, in contrast to natural transformations, conatural transformations don't compose nor have a notion of identity. Nevertheless, given a diagram $D\colon I\to C$ on $C$, one can still make $\CoNat(\Delta_{-},D)$ into a functor, by showing that the map $f^*$ gives a well-defined function $\CoNat(\Delta_Y,D)\to\CoNat(\Delta_X,D)$ between quotients, respecting the above equivalence relations. Similarly, one may define a functor $\CoNat(D,\Delta_{-})$.

The above relation takes an interesting form in the case of $\CoNat(\Delta_X,D)$: it is the quotient of the set $\coprod_{A\in I}\Hom_D(X,D(A))$ of maps $X\to D(A)$ identifying two such maps $\lambda_{A},\lambda_B\colon X\to D(A)$ whenever there exists a morphism $f\colon A\to B$ of $I$ making the diagram

commute.

Finally, one may define notions of "dual" co/limits as the co/representing objects of the functors $\CoNat(\Delta_{-},D)$ and $\CoNat(D,\Delta_{-})$.

I haven't yet figured much about these "dual co/limits", except that "dual co/products" almost never exist, since they require isomorphisms of the form $\Hom(X,A\times^{\text{dual}}B)\cong\Hom(X,A)\coprod\Hom(X,B)$, which almost never hold for all $X$. Nevertheless this still seems like a potentially interesting notion in other cases (e.g. that of "dual equalisers", in which case the above equivalence relation isn't trivial).

Have the above notions of "natural cotransformations" and "dual co/limits" been studied before in the literature? Are there any useful applications of them in mathematical practice?

Improve this question
$\endgroup$
8
  • $\begingroup$ Dual (co)products should exist frequently in the case of Ab-enriched categories, just since coproducts there are the same as products (but this is not very interesting). Perhaps there are other cases of enriched categories where these occur more frequently? Still in Ab-categories, for a pair of parallel arrows, if the top one is zero, this takes some $X$ to the set of arrows to $B$ such that everything factoring over the bottom arrow in the diagram is quotiented to zero in that set. I wonder if this could be used to encode additive quotients if one takes larger diagrams of a similar form? $\endgroup$
    – Logan Hyslop
    Nov 10, 2022 at 18:59
  • 1
    $\begingroup$ @LoganHyslop I'm quite hopeful there might be interesting examples for enriched categories, but at the same time I'm not sure/haven't checked yet how to define "dual co/limits" for bases of enrichment other than Set, since in that setting we lose constant functors (and since CoNat(F,G) isn't functorial in general, we have to construct CoNat(Delta_-,D) by hand)... $\endgroup$
    – Emily
    Nov 11, 2022 at 0:47
  • 1
    $\begingroup$ If we forgoe using an enriched constant functor, and just define $\operatorname{CoNat}(\Delta_X,D)$ as the coequalizer of $\coprod_{i}Hom_C(X,D(i))$ to the other one with whatever two arrows, then if the tensor product in V commutes with colimits, in particular coproducts and coequalizers, we should be able to define, just by the maps $Hom(X,Y)\otimes Hom(Y,D(i))\to Hom(X,D(i))$, a map on the diagram of coproducts and parallel arrows, which should descend to a $V$-functorial map on the coequalizers. I think, this doesn't give us an actual $\Delta_X$, but should let us define some analogue (?) $\endgroup$
    – Logan Hyslop
    Nov 11, 2022 at 4:38
  • 1
    $\begingroup$ Well, I guess this sort of makes it clear that in Set or similar cases, $\operatorname{CoNat}(\Delta_{(-)},D)$ is computed just as $\operatorname{colim}_{i}\operatorname{Hom}_C(-,D(i))$, a colimit of representable presheaves. So the question of when do dual (co)limits exist becomes when is a colimit of representable presheaves still representable. $\endgroup$
    – Logan Hyslop
    Nov 11, 2022 at 4:56
  • 1
    $\begingroup$ @LoganHyslop Oh very good points! I find the second one particularly illuminating as a way to think about co/limits (dual or not), by the way! $\endgroup$
    – Emily
    Nov 12, 2022 at 4:28

0

Reset to default

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.