Let $G$ be a finite non-abelian group of $n$ elements.
I would like a measure that intuitively captures the
extent to which $G$ is non-commutative.
One easy measure is a count of the non-commutative products.
For example, for $S_3$, 9 products are non-commutative,
or, 18 of the 36 entries in the multiplication table indicate
non-commutivity
(in the table, $r$=rotation; $f$=flip):
S3Table http://cs.smith.edu/~orourke/MathOverflow/S3Table.png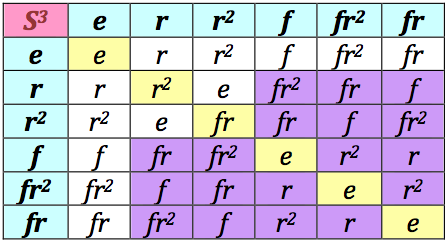
So one might say $S_3$ is 50% non-abelian.
Another idea is to determine the fewest element identifications
needed to make the group abelian. If one identifies
the elements $r$ and $r^2$ above, and calls the resulting merged element $a$,
then I believe $S_3$ is reduced to the abelian $C_2$:
S3RedC2 http://cs.smith.edu/~orourke/MathOverflow/S3RedC2.png
So one might say $S_3$ is one element identification away from being abelian.
My question is:
Is there some standard, accepted measure of how far a group is from being abelian?
Ideally such a measure would not be restricted to finite groups. Thanks for pointers!
