Of course, one might say that both $Z(G)$ and $[G,G]$, in a sense, "measure" the non-commutativity of $G$. But they are not very good "quantitative" measures.
I think what you are aiming at is a notion introduced by Turán and Erdős (Some problems of a statistical group theory IV, Acta Math. Acad. of Sci. Hung. 19 (1968), 413-435), the "probability that two elements of $G$ commute":
$$P(G) = \frac{\left|\{ (x,y)\in G\times G\mid
xy=yx\}\right|}{|G|^2}.$$
In fact, $P(G) = k/|G|$, where $k$ is the number of conjugacy classes of $G$. Gustafson proved that if $G$ is nonabelian then $P(G)\leq 5/8$, and extended the notion to compact groups using Haar measure (W. Gustafson, What is the probability that two group elements commute? American Math. Monthly 80 (1973) 1031-1034). MacHale proved that certain values cannot occur: if $P(G)\gt \frac{1}{2}$, then $P(G) = \frac{1}{2} + \left(\frac{1}{2}\right)^{2s+1}$; and $P(G)$ cannot satisfy $\frac{7}{16} \lt P(G) \lt \frac{1}{2}$. Joseph proved that if $G$ is not commutative and $p$ is the smallest prime that divides $|G|$, then $P(G)\leq \frac{p^2+p-1}{p^3}$ (K.S. Joseph, Commutativity in non-abelian groups, PhD thesis, 1969, UCLA). There's been some other work on this.
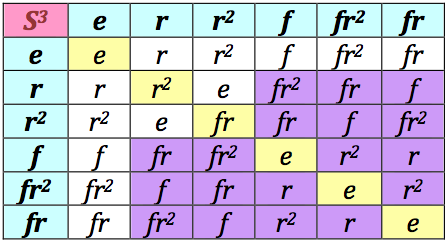
In the case of $S_3$. $|G|=6$, and the set of pairs $(x,y)$ with $xy=yx$ is, as you note, $18$, so the probability that two elements commutes is precisely your "50% nonabelian".
Your second notion seems to be that of looking at $G/[G,G]$, which is the "largest" quotient of $G$ which is abelian.
Added: Since I edited to fix the accent on Erdős, I'll take the opportunity to add some references:
- Desmond MacHale, How commutative can a non-commutative group be?, Math. Gazette 58 (1974), 299-202.
- David J. Rusin, What is the probability that two elements of a finite group commute?, Pacific J. Math 82 (1979), no. 1, 237-247.
- Robert Guralnick and Geoff Robinson, On the commuting probability in finite groups, J. Algebra 300 (2006), no. 2, 509-528, MR 2228209 (2007g:60011); Addendum, J. Algebra 319 (2008), no. 4, 1822.