10
$\begingroup$

In general, one extracts a manifold invariant from a TQFT by interpreting the closed manifold as a bordism from the empty set to the empty set. The TQFT sends this bordism to a homomorphism of the ground field, which is a number. Such invariants are always multiplicative under disjoint union, this is a consequence of the TQFT being a monoidal functor: $$\mathcal{Z}(M_1 \sqcup M_2) = \mathcal{Z}(M_1) \otimes \mathcal{Z}(M_2) = \mathcal{Z}(M_1) \cdot \mathcal{Z}(M_2)$$

Some TQFTs, like the Crane-Yetter invariant (but not, say, the Turaev-Viro model) give manifold invariants that are multiplicative under connected sum $\#$.

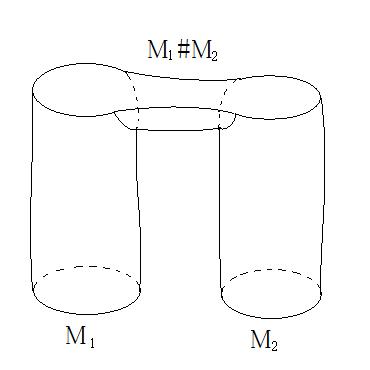
One way to see this is to notice that they can be defined (for connected manifolds) with Kirby calculus: Given a manifold, choose a handle decomposition and consider its link diagram. The diagram is then labelled with morphisms from a ribbon fusion category and the whole diagram is evaluated as a morphism from the monoidal identity to itself, again a number. Now the evaluation of the disjoint union of two link diagrams must then give the product of the evaluations of the respective diagrams, since a ribbon fusion category is monoidal. But the disjoint union of two link diagrams of manifolds $M_1$ and $M_2$ is the link diagram of the connected sum $M_1 \# M_2$!

Which leads me to believe that this multiplicativity secretly comes from monoidality of some functor again. Is there a category of bordisms where the monoidal product of morphisms (=bordisms) is the connected sum, and not the disjoint union? Are such TQFTs actually monoidal functors from this bordism category to $\mathrm{Vect}$?

A related, noncategorical question was asked here: Monoid structure of oriented manifolds with connect sum

Improve this question
$\endgroup$
8
  • $\begingroup$ Is it known for which kinds of manifolds is connected sum bordant to the disjoint sum? $\endgroup$
    – მამუკა ჯიბლაძე
    Aug 25, 2014 at 14:24
  • $\begingroup$ I'm assuming you want to construct a category whose objects are manifolds, and morphisms are bordisms, such that the tensor product is the connected sum. You probably already know this anyway, but here goes. We know that the connected sum $\#$ is associative, so that $\alpha_{\mathscr{M,N,O}}:\mathscr{M\#(N\# O)=(M\# N)\# O}$, where $\mathscr{M,N,O}$ are all oriented, connected, compact, $n$-dimensional manifolds... $\endgroup$
    – user62675
    Aug 25, 2014 at 22:12
  • 1
    $\begingroup$ ... The identity is given by $I=S^n$, the $n$-sphere; hence $\lambda_\mathscr{M}:\mathscr{M}=S^n\#\mathscr{M}$, and since $\mathscr{M\#N=N\#M}$, there is also an isomorphism $\rho_\mathscr{M}:\mathscr{M}\#S^n=\mathscr{M}$. Now you need to show the pentagon and the triangle identities hold. Since I'm travelling now, I must take leave. $\endgroup$
    – user62675
    Aug 25, 2014 at 22:13
  • $\begingroup$ Here is a problem: The connected sum of two cylinders over $M_1$ and $M_2$ is not the cylinder over $M_1 \sqcup M_2$. So one must modify the monoidal product over objects as well. $\endgroup$
    – Manuel Bärenz
    Aug 26, 2014 at 16:50
  • 5
    $\begingroup$ @Turion I think მამუკა ჯიბლაძე has answered your question already, but I think it's worth commenting that connected sum is not a bifunctor. Indeed $M \# N$ depends on the choice of a ball in $M$ and in $N$, so it's only well defined up to a noncanonical isomorphism. $\endgroup$
    – Dan Petersen
    Aug 27, 2014 at 6:51

2 Answers 2

Reset to default
6
$\begingroup$

If the dimension of $Z(S^{n-1})$ is greater than 1, then the TQFT is not even approximately multiplicative under connect sum.

If $Z(S^{n-1})$ is 1-dimensional, then a simple cut and paste argument shows that $$ Z(M_1 \sharp\, M_2) = Z(M_1 \sqcup M_2) \,/\, Z(S^n) = Z(M_1) \cdot Z(M_2) \,/\, Z(S^n) . $$ So in this case $Z$ is multiplicative under direct sum iff $Z(S^n) = 1$. (If $Z(S^n) \ne 1$ we might say that the theory is approximately multiplicative under connect sum.)

When $n$ is even, the Euler characteristic of $S^n$ is non-zero and we can tensor with an Euler characteristic theory to arrange that $Z(S^n) = 1$.

When $n$ is odd, the Euler characteristic of $S^n$ is zero and there is no way to tweak things so that $Z(S^n) = 1$. Turaev-Viro and Witten-REshetikhin-Tureav theories fall into this class.

I'll also remark that if $M_i$ is not connected, then $M_1 \sharp\, M_2$ is not well-defined, even up to homeomorphism. But nevertheless the above claims about $Z(M_1 \sharp\, M_2)$ are true, for any choice of the ambiguous connect sum.

Improve this answer
$\endgroup$
10
  • $\begingroup$ It occurs to me that perhaps you were asking about theories which are multiplicative under connect sum but not disjoint union. In my answer I was making the usual assumption about multiplicativity under disjoint union, and considering the case where in addition to that we have multiplicativity under connect sum. $\endgroup$
    – Kevin Walker
    Aug 27, 2014 at 14:12
  • $\begingroup$ Thanks, that pretty much characterises TQFTs that are multiplicative under connected sum. I'm fine with keeping the additional assumption of multiplicativity under disjoint union. Do you think your answer suggests that there is some monoidal structure on (connected) cobordism given by connected sum? If the monoidal product on objects was connected sum, it would imply $Z(S^{n-1}) \cong Z(S^{n-1}\#S^{n-1}) \cong Z(S^{n-1}) \otimes Z(S^{n-1}) \implies \dim Z(S^{n-1}) = 1$. $\endgroup$
    – Manuel Bärenz
    Aug 27, 2014 at 14:23
  • 1
    $\begingroup$ There are probably various ways of defining monoidal categories using these ingredients, but I can't think of one where the monoidal product is connected sum for both objects (dimension $n-1$) and morphisms (dimension $n$). $\endgroup$
    – Kevin Walker
    Aug 27, 2014 at 14:42
  • $\begingroup$ If I take a $B^n \subset M^n$ with $B^{n-1}$'s in both boundary components, for both bordisms, I should be able to connect-sum them such that their boundaries are also being connect-summed, right? That's the monoidal product I have in mind, are there any others you can think of? $\endgroup$
    – Manuel Bärenz
    Aug 27, 2014 at 14:53
  • 1
    $\begingroup$ On second thought, your proposed definition is ambiguous. The choice of $B^n \subset M^n$ amounts to a choice of arc connecting the two boundary components, and different isotopy classes of arc can yield different results. $\endgroup$
    – Kevin Walker
    Aug 27, 2014 at 18:24
0
$\begingroup$

According to the Manifold Atlas, connected sum is bordant to the disjoint union for fairly general classes of manifolds. The proof is more or less clear from the picture given there enter image description here

With slightly more care, I'm sure that the connected sum and the disjoint union are naturally isomorphic as bifunctors, so there is a monoidal structure wrt connected sum.

In any case, values of any QFT on the disjoint union and on the connected sum are "the same".

(Edit) The comments of Dan Petersen to the OP and of Qiaochu Yuan to this post indicate that this answer is not really correct. I am still leaving it since I still think that existence of the above bordism is relevant for the question.

Improve this answer
$\endgroup$
3
  • 3
    $\begingroup$ That last sentence doesn't sound right to me. You certainly can't expect this property of an $n$-dimensional TQFT if $\dim Z(S^{n-1}) \neq 1$ (for an explicit example, take $n = 2$ and consider Dijkgraaf-Witten theory for a nontrivial group). The existence of a bordism is not enough because a TQFT need not send a bordism to an isomorphism. $\endgroup$
    – Qiaochu Yuan
    Aug 27, 2014 at 7:16
  • $\begingroup$ @QiaochuYuan Oh I see, thank you. Still I'll leave a version of the answer - there must be some implications of the existence of this bordism... $\endgroup$
    – მამუკა ჯიბლაძე
    Aug 27, 2014 at 7:21
  • 2
    $\begingroup$ Also there is a problem with dimensions; the source and target of this bordism are dimension $n-1$ but the question is about connected sums of manifolds in the top dimension $n$. $\endgroup$
    – Qiaochu Yuan
    Aug 27, 2014 at 18:41

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.