When has the scaffolding been more important than the completed building?

Question

Niels Abel once said⁽¹⁾ of Gauss, "He is like the fox, who effaces his tracks in the sand with his tail." to which Gauss replied, "No self-respecting architect leaves the scaffolding in place after completing his building."

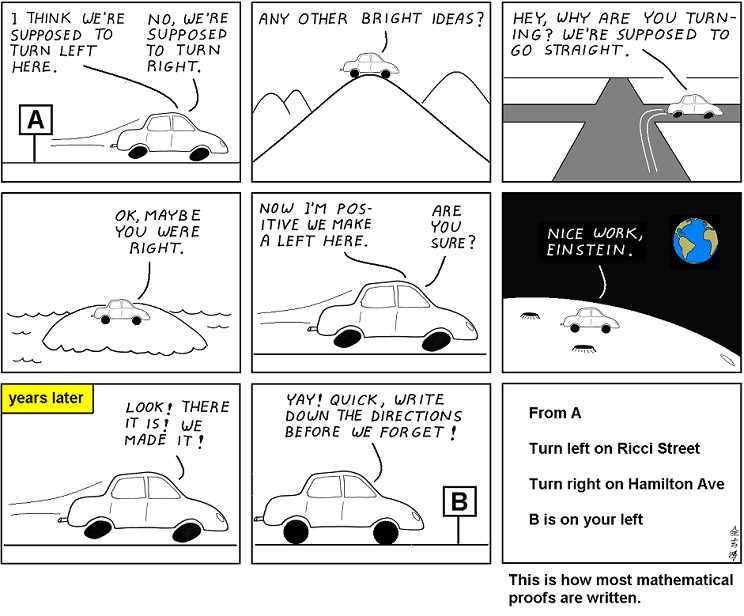
This is also illustrated by this Abstruse Goose comic (originally licensed CC BY-NC 3.0 US DEED):

Of course, and with all due respect to Gauss, I've encountered situations where I wished I knew just how an author reached an argument, much more than I was interested in the eventual result. While it's always pleasant to marvel at the elegance of a proof, it's often the case that I want to reach a slightly different result for which the original proof breaks down. In these situations, I always wonder whether the author's original insight, which may be hidden by years of whittling the argument into the elegant proof I'm reading, would help.

What are some historically important examples where seeing the scaffolding around the completed building proved much more important than seeing the building itself?

Update: Based on the comments, let me be more precise on what I'm looking for. This would include examples where someone proved some (important?) theorem, then (much?) later, someone else rediscovered the insights that led to the proof and built a new theory that eclipsed the original theorem. Or situations that are similar, even if they do not fit exactly this description.

---

(1) Simmons, George Finlay (1992). Calculus Gems. New York: McGraw Hill. p. 177. ISBN 0-88385-561-5. I originally read this on Wikipedia: https://en.wikipedia.org/wiki/Niels_Henrik_Abel#Contributions_to_mathematics

Answer 1

Ramsey Theory should count. Ramsey needed his theorem for a proof of a special case of the decision problem for first-order logic — which in the general case soon turned out to be unsolvable — but from the same theorem arose a large branch of combinatorics.

Answer 2

"examples where someone proved some (important?) theorem, then (much?) later, someone else rediscovered the insights that led to the proof and built a new theory that eclipsed the original theorem."

According to this updated criterion, Grove and Shiohama proved some basic results about critical points of distance functions in

Grove, Karsten; Shiohama, Katsuhiro. A generalized sphere theorem. Ann. of Math. (2) 106 (1977), no. 2, 201–211

and applied it to prove "a generalized sphere theorem" (as the title indicates).

Gromov realized the hidden potential of this new notion, and pushed it through to obtain far more general results in

Gromov, Michael. Curvature, diameter and Betti numbers. Comment. Math. Helv. 56 (1981), no. 2, 179–195.

Gromov's paper is of fundamental importance in modern Riemannian geometry. It is cited by almost 400 papers.

Answer 3

I see several different ways of interpreting the question.

1. The comic seems to be talking about mistakes (false starts, blind alleys, etc.) made along the way to a mathematical discovery. I think that it's relatively rare that bringing to light all these mistakes leads to significant mathematical progress. It might be comforting to us lesser lights when we learn that a revered, great mathematician also made mistakes, but emotional comfort is not the same as mathematical insight. Having said that, I'd point to another MO question about interesting mathematical mistakes for some possible answers of this sort.

2. There have been times when mathematicians would intentionally conceal their methods of arriving at their results, in order to gain an advantage over their rivals. A historically important example was Scipione del Ferro's method for solving cubic equations. I'm sure that many other examples of this type could be listed, but they are perhaps less interesting because it is obvious to everyone from the outset that the secret technique is more important than any particular application of it.

3. Another scenario is that someone hides a technique not to protect a trade secret but because conventions of mathematical writing style encourage the hiding. Examples of this sort are perhaps closest to what the OP wants, but it's not so easy to give examples, because if a different researcher later comes up with a technique that yields the same result in a less mysterious way, how do we know that the later researcher is rediscovering the first researcher's technique, as opposed to discovering a brand new technique? For example, I find Spivak's version of the Heath-Brown/Zagier proof that a prime of the form $4n+1$ is the sum of two squares to be enormously enlightening, but it may be a matter of debate whether Spivak found something new, or rediscovered some hidden scaffolding. In a few cases, there is little debate because it is the original researcher who later lays bare the hidden scaffolding, as in Ryan Williams's Casual tour around a circuit complexity bound, but such examples seem to be rare.

4. Maybe the most interesting case occurs when the reason for hiding the scaffolding is that the scaffolding is genuinely difficult to put into words. Terry Tao wrote a fantastic blog post about Jean Bourgain, in which he explains that Bourgain had a large store of techniques that he drew upon, and that Bourgain's papers were often difficult to read if you were not fluent with those techniques. But Bourgain was not trying to hide anything; the problem was that the techniques were so versatile and protean that spelling them out in full detail was nearly impossible.

I'd be interested in other examples of Case 4, by which I mean situations where someone takes the time to formally or semi-formally codify a set of powerful techniques that are implicitly used by experts but not spelled out in black and white. Off the top of my head, I can think of the Wilf–Zeilberger method, Christian Krattenthaler's Advanced determinant calculus, and Scott Aaronson's step-by-step instructions on how to upper-bound the probability of something bad, but there are surely many other examples.

Answer 4

A classical example is the Riemann-Siegel formula, even though it hardly can be assumed to be more important than the building itself.