Graphs with many edges avoided by Hamiltonian cycles

Question

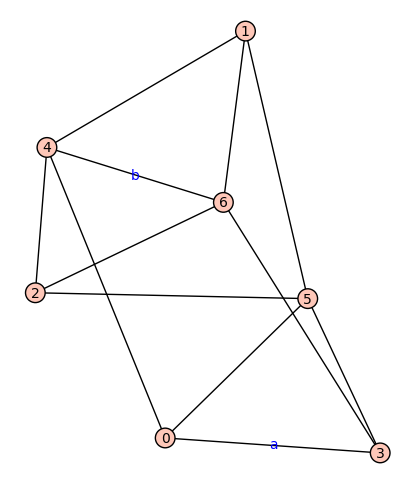
Let $G$ be a $3$-connected Hamiltonian graph with at least one edge that belongs to each H-cycle of $G$. Some authors (e.g. in the link given here) call such an edge an a-edge and an edge that belongs to no H-cycle of $G$ a b-edge. Let $a(G)$ and $b(G)$ denote the number of a-edges and b-edges, respectively. Define $\rho(G)=\dfrac{b(G)}{a(G)} $.

• Are there good (or even sharp) upper bounds for $\rho(G)$ ? Maybe $\rho(G)<1$?

Such graphs can be constructed e.g. using certain non-Hamiltonian graphs like the so-called Tutte fragment $T$ or the “Petersen fragment” $P$, the latter obtained from the Petersen graph by adding a vertex on each of three consecutive edges and an edge leaving at each of those vertices. These edges are labelled by $1,2,3$.

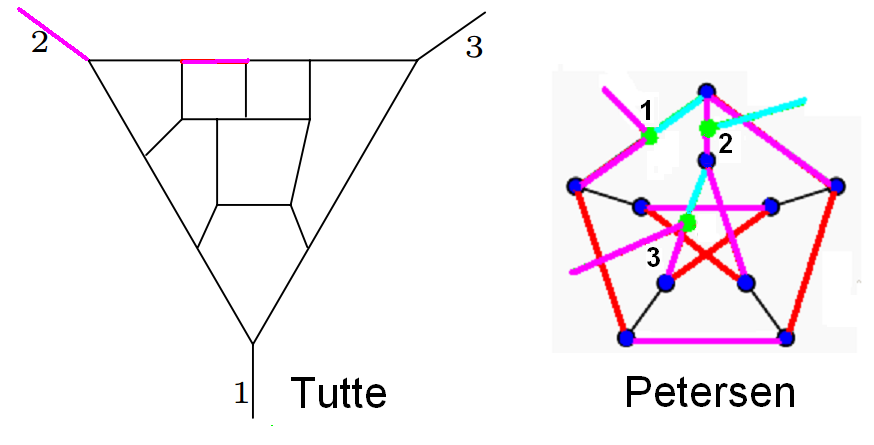
It is easy to see that $T$ does not admit a H-path between 1 and 3, whereas $P$ admits no H-path starting at 2, only two H-paths between 1 and 3 (one consists of the violet and the red edges, the other one of the violet and the black edges). $T$ has two a-edges (marked in violet) and no b-edges; $P$ has nine a-edges (violet) and three b-edges (light blue).
The simplest $3$-connected Hamiltonian graphs obtained from these are a prism over the big “triangle” of $T$ with $a(G)=3$ and $b(G)=0$ (note that this one is even planar) and likewise a prism over $P$, which has $a(G)=16$ and $b(G)=5$.

By taking a Hamiltonian graph and replacing certain cubic vertices by $T$ or $P$, we can impose restrictions on the H-cycles and obtain graphs with various values of $a(G)$ and $b(G)$.
If we start with the wheel $W_{n}$ and replace one vertex by a $T$ in such a way that the spike becomes an a-edge, the resulting graph 'keeps' only two of the H-cycles of $W_n$ and has $\rho(G)=\dfrac{n-3}{n}$. I wonder if this is best possible. So if generally $\rho(G)<1$ holds, that would be sharp.

What about the maximum if we consider only cubic graphs ?
If we start with the prism over $K_3$ and make one ‘vertical' edge a b-edge by replacing one vertex with a $P$, we get a graph with a unique$^*$ H-cycle and $\rho(G)=\dfrac{5}{13}\approx.3846 $.
If we start with the dodecahedron and 'block' three well chosen edges (i.e. make them into b-edges) by replacing three vertices with $P$'s, we get a graph with a unique$^*$ H-cycle and $\rho(G)=\dfrac{16}{41}\approx.3902 $, slightly larger.
Starting with a truncated icosahedron (soccerball), we can still do better. It depends on how many edges have to be blocked by using $P$'s to remain with a unique$^*$ H-cycle: if there are $k$ such edges and the resulting graph $G$ is unique$^*$ Hamiltonian, it will have $\rho(G)=\dfrac{30+2k}{60+7k} $, which is equal to $\dfrac{16}{41}$ for $k=9$ and gets bigger as $k$ decreases. I've checked that $k=7$, thus $\rho(G)=\dfrac{44}{109}\approx.4037 $, is possible. (Note that in the drawing given in the link, only the green and black 1-factors yield a H-cycle.)

$^*$ Edit: "unique" is meant w.r.t. the H-cycles of the original graph, because inside the instances of $P$ there are of course several ways of making H-paths through them.

Of course I don't claim that this method yields the best possible results. So the question:

• Are there cubic, 3-connected graphs with $\rho(G)$ even bigger than that?

Answer 1

The first counterexample given by @joro gives rise to the following family $G_k$ of graphs with $\rho(G_k)=k$ : $G_k$ has $n=4k+3$ vertices numbered $0,1,\dots,n-1$ forming a H-cycle (imagine a regular n-gon embedded such that the vertex $2k+1$ is on the bottom), plus the ‘horizontal’ chords $(2j-1,4k+3-2j)$ for $j=1,...,k$ (call their set $B$) and the other chords $(j,2k+1+j)$ for $j=0,...,2k+1$. It is not hard to see that $(4k+2,0)$ is an a-edge. As the graph without this edge and without $B$ is bipartite, all edges of $B$ must be b-edges. It remains to check that for each other edge, there is a H-cycle that doesn’t contain it.

For the second question, as @Martin Tancer and @nvcleemp have pointed aout, $\rho(G)\le1/2$ for cubic graphs. The following construction comes arbitrarily close to $1/2$ :

For $n=2k$, start with a H-cycle $0,...,2k-1,0$ and add the ‘horizontal’ chords $(j,2k-j)$ for $j=1,...,k-1$ and the ‘vertical’ chord $(0,k)$. Replace the vertex $k$ with an instance of $P$ that blocks the vertical chord. Then it is easy to see (starting at the vertex $0$) that the horizontal chords cannot be part of a H-cycle. So this graph has $a(G)=2k+7$ (the original cycle plus 7 inner edges of $P$) and $b(G)=k+1$ (the horizontal chords plus 2 inner edges of $P$).

So both original questions are answered, thanks to your input. Remains the interesting question raised by joro what can be said about $\rho(G)$ for 4-regular graphs.

Answer 2

The computer found counterexamples to $\rho(G)<1$.

Despite verification, I am not sure this is correct.

$G_1$ on $7$ vertices, $G_2$ on $11$ vertices. $\rho(G_1)=1,\rho(G_2)=2$

$G_1$:

edges=[(0, 3), (0, 4), (0, 5), (1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 5), (3, 6), (4, 6)]
A=[(0, 3)]
B=[(4, 6)]

$G_2$:

edges=[(0, 5), (0, 6), (0, 7), (1, 6), (1, 7), (1, 8), (2, 6), (2, 8), (2, 9), (3, 7), (3, 9), (3, 10), (4, 8), (4, 9), (4, 10), (5, 9), (5, 10), (6, 8), (7, 10)]
A=[(0, 5)]
B=[(6, 8), (7, 10)]

Plot of $G_1$: