Minimum distance between Hamiltonian cycles in cubic Hamiltonian graph

Question

It is $NP$-hard to find constant factor approximation of longest cycle in cubic Hamiltonian graphs. Therefore, finding a Hamiltonian cycle in a cubic Hamiltonian graph is NP-hard.

By Smith's theorem, cubic Hamiltonian graph contains at least two Hamiltonian cycles. Therefore, finding a Hamiltonian cycle in a cubic Hamiltonian graph is NP-hard. Given cubic graph on $N$ nodes:

What is the best lower bound on the minimum Hamming distance between two Hamiltonian cycles (each Hamiltonian cycle contains $N$ nodes) in cubic Hamiltonian graph?

Here Hamming distance between two Hamiltonian cycles is the is $N-$ the number of shared edges. $N$ is the number of nodes in the graph. The upper bound is $N/2$.

EDIT: I conjecture that it is at least $\Omega(\log N)$ and I even conjecture a tighter lower bound of $\Omega( \epsilon N)$ for some constant $\epsilon \gt 0$.

Answer 1

Let me maybe just formulate the comment as an answer.

It is easy to see that the lower bound can't be 1. Assume that $H_1$ contains the edge $e$, and $H_2$ does not contain $e$. If the edge $e$ is not contained in a triangle, then it has 4 adjacent edges. Then $H_2$ has to contain all 4 of these edges, while $H_1$ can only contain 2 of them, so the hamming distance is at least 2. If the edge $e$ is contained in a triangle, then $H_1$ and $H_2$ can share at most one edge of the triangle and at most one of the incoming edges of the triangle, or no edge of the triangle and two of the incoming edges. In either case the hamming distance is at least 2.

In case of the $K_4$ the minimum Hamming distance is 2. To construct a cubic graph in which the minimum hamming distance is 2, just take any hamiltonian cubic graph. Remove an edge that is contained in a hamiltonian cycle. Take a $K_4$ and remove an edge. Connect the vertices of degree two in both graphs to get a new cubic graph. The new graph is hamiltonian and contains two hamiltonian cycles that only differ in the edges in the $K_4$, so the hamming distance is 2.

Of course the graphs above have girth 3, so it might be possible to give a better lower bound as a function of the girth of the graph.

Edit: Maybe this illustration will make things more clear. Take any hamiltonian cubic graph and take an edge that is contained in a hamiltonian cycle (shown in red at the top). Insert a $K_4$ minus an edge into that edge. The new graph has two hamiltonian cycles (shown in red at the bottom left and right) which have hamming distance 2. You can do this for any cubic graph which has a hamiltonian cycle so you can get any number of vertices and still have minimum hamming distance 2.

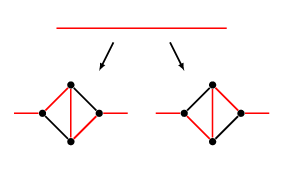
Edit 2: Since both $K_4$ and $K_{3,3}$ contain hamiltonian cycles with hamming distance 2, and the construction above adds 4 vertices, we have that for all $n\geq4$, there exists a cubic hamiltonian graph $G$ on $n$ vertices such that $G$ contains at least two hamiltonian cycles at hamming distance 2.