26
$\begingroup$

The following problem is only tangentially related to my present work, and I do not have any applications. However, I am curious to know the solution -- or even to see a lack thereof, indicating that the problem may be worth a serious research.

Let $\mathcal F$ denote the class of all functions $f\colon[0,1]\to{\mathbb R}$ satisfying the inequality $$ f(tx+(1-t)y) \le tf(x) + (1-t)f(y) + |y-x|, \ x,y,t \in [0,1] $$ and the boundary condition $\max\{f(0),f(1)\}\le 0$.

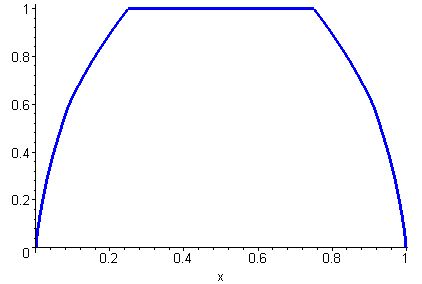
Substituting $x=0$ and $y=1$, we see that all functions from $\mathcal F$ are uniformly bounded from above by $1$, and we let $$ F(x) := \sup \{ f(x)\colon f\in {\mathcal F} \}. $$ An interesting observation is that the function $F$ itself belongs to $\mathcal F$; hence, it is the pointwise maximal function of this class. What is this function, explicitly?

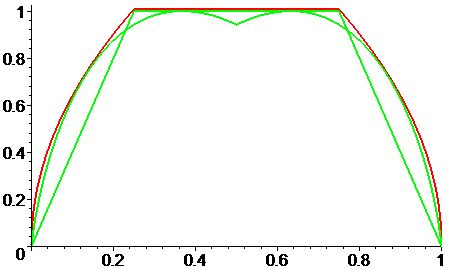
It is not difficult to see that $F$ is continuous on $[0,1]$, symmetric around $x=1/2$, positive on $(0,1)$, and vanishing at $x=0$ and $x=1$. Substituting $t=x$ and $y=0$ and renaming the variables in the resulting estimate gives $F(x)\le 2\sqrt x$; hence, indeed, $$ F(x) \le \min\{2\sqrt x,1,2\sqrt{1-x} \}. $$ On the other hand, the functions $\min\{4x,1,4(1-x)\}$ and $ex\ln(1/x)$ belong to $\mathcal F$, implying $$ F(x) \ge \min\{4x,1,4(1-x)\} $$ and $$ F(x) \ge \max \{ ex\ln(1/x), e(1-x)\ln(1/(1-x))\}, $$ for all $x\in[0,1]$.

The graphs of the bounding functions in the right-hand sides:

the graphs (source)

(Thus, the graph of $F$ resides somewhere between the highest of the green curves and the red curve.)

Comparing the estimates, we see that $F(x)=1$ for $x\in[1/4,3/4]$, and $0<F(x)<1$ for $x\in(0,1/4)$ and also for $x\in(3/4,1)$. I have more estimates and observations of this sort. Say, I can show that if $x=e^{-k}$, then $F(x)=ex\ln(1/x)$; that is, $F(e^{-k})=ke^{1-k}$ for $k\ge 2$. Another funny fact is that for any function $f\in{\mathcal F}$ (and in particular for the function $f=F$) one has $$ f(tx+(1-t)y) \le tf(x) + (1-t)f(y) + F(t)|y-x|, \ x,y,t \in [0,1]. $$ However, with all these partial results and rather tight bounds, so far I was unable to find $F(x)$ in general. Any ideas?

Improve this question
$\endgroup$
1
  • $\begingroup$ Choosing a finite subdivision $0=x_0<x_1<\dots<x_n=1/4$, setting $y_0=0,y_n=1$ and writing all possible inequalities for the function $\{x_0,\dots,x_n\}\longmapsto \mathbb R_{\geq 0}$ defined by $f(x_i)=y_i$, the largest possible value $y_i$ (which can be computed by the simplex algorithm) of the solution polytope (defined by $y_i\geq 4x_i$ and all possible inequalities given by the problem) is an upper bound for $F(x_i)$ (and converges to $F(x_i)$ if $\max_i(x_{i+1}-x_i\longrightarrow 0$). $\endgroup$
    – Roland Bacher
    Feb 10, 2012 at 13:35

1 Answer 1

Reset to default
12
$\begingroup$

It may be a little uncommon to post an answer to one's own question, but for a good record-keeping I think it is worth mentioning that a complete and very explicit answer is now known. The function in question is given by $$ F(x) = \min \{ k\|x\|^{1-1/k}\colon k\ge 1 \}, $$ where $k$ runs over all positive integers, and $\|x\|=\min\{x,1-x\}$. The graph of this function looks like this:

the graph (source)

The proof and applications can be found here.

Improve this answer
$\endgroup$
1
  • 4
    $\begingroup$ (btw, it is not uncommon to post an answer to one's own question. it is in fact encouraged!) $\endgroup$
    – Willie Wong
    Nov 26, 2013 at 12:57

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.

Not the answer you're looking for? Browse other questions tagged or ask your own question.