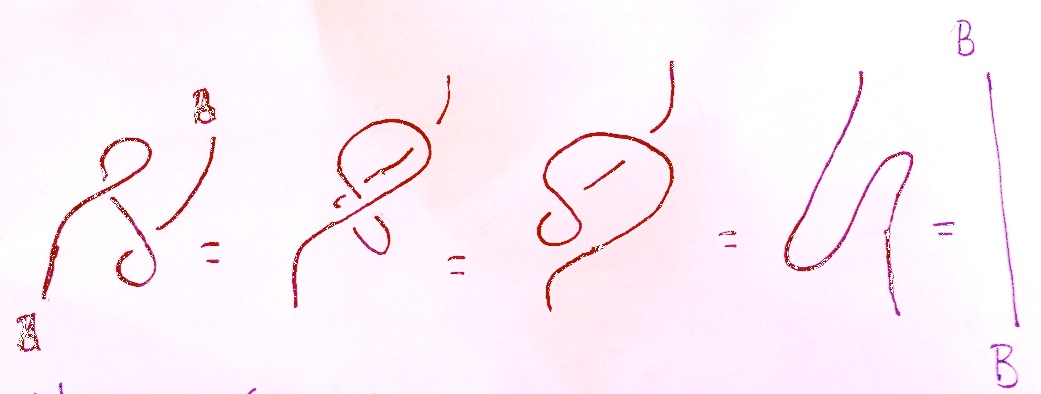Why is a braided left autonomous category also right autonomous?

Question

In Selinger, P. A survey of graphical languages for monoidal categories (New Structures for Physics, Springer, 2011, 813, 289-233), it is stated that:

Lemma 4.17 ([23, Prop. 7.2]). A braided monoidal category is autonomous if and only if it is right autonomous.

Proof. If $\eta : I \rightarrow B \otimes A$ and $\epsilon : A \otimes B \rightarrow I$ form an exact pairing, then so do $c^{-1}_{A,B} \circ \eta : I \rightarrow A \otimes B$ and $\epsilon \circ c_{B,A} : B \otimes A \rightarrow I$. Therefore any right dual of $A$ is also a left dual of $A$.

(The reference [23] is A. Joyal and R. Street. Braided tensor categories. Advances in Mathematics, 102:20–78, 1993.)

I don't understand why $c^{-1}_{A,B} \circ \eta$ and $\epsilon \circ c_{B,A}$ form an exact pairing. We need to prove that $((\epsilon \circ c_{B,A}) \otimes 1_B) \circ (1_B \otimes (c^{-1}_{A,B} \circ \eta)) = 1_B$ and $(1_A \otimes (\epsilon \circ c_{B,A})) \circ ((c^{-1}_{A,B} \circ \eta) \otimes 1_A) = 1_A$, but I can't see what axiom can be applied here.

Any hint is welcome.

Answer 1

Here's a hint: what you should probably use here is the method of string diagrams (due to Joyal and Street, but by now ubiquitous). In other words, draw a picture in terms of tangles; you will see two crossings, and you want to apply a series of Reidemeister II and III moves to make those crossings cancel out; these moves can be justified in any braided monoidal category. (It turns out that what you want to prove is an algebraic form of the Whitney trick applied to ordinary knots; see Kauffman's On Knots; look carefully on page 172.)

If this hint is insufficient, I can come back and explain more (and I probably will if no one else answers; I'd have to sit down and LaTeX the commutative diagram though). The Reidemeister II move is essentially based on invertibility of the braiding $c$, and the Reidemeister III move on naturality of $c$ and the braiding axiom (a hexagonal coherence condition, but really a triangular coherence condition if you assume, as you may, that the associativity is strict).

Edit: I have written out a complete derivation here.

Answer 2

(Apologies for problems with the LaTeX; I’m on a dodgy internet connection and having trouble previewing to fix it. Will attempt to fix it later when home.)

With any question like this — deriving an equation in some class of structures with a graphical language — my modus operandi is:

• work it out in string diagrams;
• translate back to algebraic language, if necessary.

This one comes out in string diagrams as:

(Note that my diagrams go bottom-to-top for morphisms, and left-to-right for tensoring.) Translating this gives:

\begin{align} & \mathrel{\phantom{=}} (\epsilon \otimes B) \cdot (c_{B,A} \otimes B) \cdot (B \otimes c_{A,B}^{-1}) \cdot (B \otimes \eta) \\ \quad & = (\epsilon \otimes B) \cdot (A \otimes c^{-1}_{B,B}) \cdot (c^{-1}_{A,B} \otimes B) \cdot (B \otimes c_{B,A}) \cdot (c_{B,B} \otimes B) \cdot (B \otimes \eta) \\ \quad & = (\epsilon \otimes B) \cdot (A \otimes c^{-1}_{B,B}) \cdot (c^{-1}_{A,B} \otimes B) \cdot (\eta \otimes B) \\ \quad & = (B \otimes \epsilon) \cdot (\eta \otimes B) \\ \quad & = 1_B \end{align}

Here the first step is by the “Yang-Baxter” hexagon equation for braids; the second uses the fact that $(B \otimes c_{B,A}) \cdot (c_{B,B} \otimes B) = c_{B,B \otimes B}$, plus the naturality of braiding against $\eta$; the third is similar to the second; and the last is the triangle equality for the original pair of duals.

The other triangle equality for the new pairing is similar.

(To be honest, I often use this sketch-then-algebraise approach even when I don’t know yet if the graphical language is formally valid in the setting — it can still be very helpful for quickly finding algebraic proofs, and if I’ve used some illegal manipulation, then I’ll find that out when I try to translate it.)